题目内容
3.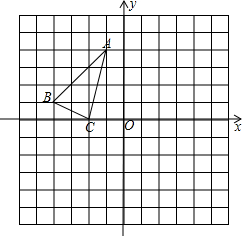 △ABC在平面直角坐标系中的位置如图所示,顶点坐标分别为A(-1,4),B(-4,1),C(-2,0),画出△ABC绕点A逆时针旋转90°后的△AB1C1,并直接写出点B旋转到点B1所经过的路线长度(结果保留π).
△ABC在平面直角坐标系中的位置如图所示,顶点坐标分别为A(-1,4),B(-4,1),C(-2,0),画出△ABC绕点A逆时针旋转90°后的△AB1C1,并直接写出点B旋转到点B1所经过的路线长度(结果保留π).
分析 分别将点B、C绕点A逆时针旋转90°后得到点B1、C1,然后顺次连接,并根据弧长公式求出点B旋转到点B1所经过的路线长度.
解答 解:所作图形如图所示:
∵AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴点B旋转到点B1所经过的路线长度l=$\frac{90π×3\sqrt{2}}{180}$=$\frac{3\sqrt{2}}{2}$π.
点评 本题考查了根据旋转变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接,注意掌握弧长公式.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a0=1 | B. | x2÷x3=$\frac{1}{x}$ | C. | (-$\frac{x}{y}$)2=-$\frac{{x}^{2}}{y}$ | D. | a4÷2-1=$\frac{1}{2}$a4 |
8.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (a3)2=a5 | C. | (a+3)2=a2+9 | D. | -2a2•a=-2a3 |
12.下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{48}$ | D. | $\sqrt{32}$ |