题目内容
如图,矩形OABC,B(9,6),点A,点C分别在x轴,y轴上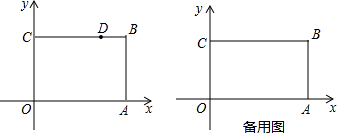 ,D为BC上一动点,把△OCD沿OD对折,C点落在点P处
,D为BC上一动点,把△OCD沿OD对折,C点落在点P处
(1)当点P在OA上时,求tan∠DAB;
(2)当点P在AC上时,求D点坐标;
(3)当点P在直线y=2x-6上时,求D点坐标.
解:(1)由题意得:OC=AB=6,OA=CB=9,
当点P在OA上时,
四边形OPDC为正方形,
∴CD=OC=6,
∴BD=3,
∴tan∠DAB= =
=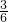 =
= ;
;
(2)当点P在AC上时,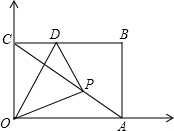
OD⊥AC,
∴∠COD=∠ACB,
∴△OCD∽△CBA,
∴ =
=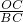 ,即
,即 =
=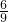 ,
,
∴CD=4,
∴D点坐标为:(4,6);
(3)过点P作OA于N,交BC于M,设P(x,2x-6),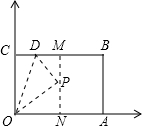
Rt△OPN中,ON2+PN2=OP2,
即x2+(2x-6)2=36,
解得:x1=0,x2= ,
,
∴ON= ,
,
PN=2x-6= ,
,
∴PM=6-PN= ,
,
易证△DPM∽△PON,
∴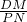 =
=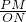 ,
,
即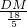 =
=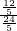 ,
,
∴DM= ,
,
∴CD=CM-DM=ON-DM=
 =3,
=3,
∴D(3,6).
分析:(1)根据题意得出四边形OPDC为正方形,求出CD=OC=6,BD=3,即可证出tan∠DAB的值;
(2)根据OD⊥AC,得出∠COD=∠ACB,△OCD∽△CBA,即可求出CD的值,从而得出D点的坐标;
(3)先过点P作OA与N,再设P(x,2x-6),在Rt△OPN中,根据x2+(2x-6)2=36,解出x的值,从而得出PM的值,再证明△DPM∽△PON,得出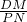 =
=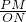 ,求出DM=
,求出DM= ,所以CD=CM-DM,从而求出D点的坐标.
,所以CD=CM-DM,从而求出D点的坐标.
点评:此题考查了相似三角形的判定与性质;解题的关键是根据锐角三角函数的定义和相似三角形的判定与性质进行解答,特别注意P点的位置.
当点P在OA上时,
四边形OPDC为正方形,
∴CD=OC=6,
∴BD=3,
∴tan∠DAB=
 =
=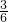 =
= ;
;(2)当点P在AC上时,

OD⊥AC,
∴∠COD=∠ACB,
∴△OCD∽△CBA,
∴
 =
=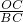 ,即
,即 =
=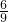 ,
,∴CD=4,
∴D点坐标为:(4,6);
(3)过点P作OA于N,交BC于M,设P(x,2x-6),

Rt△OPN中,ON2+PN2=OP2,
即x2+(2x-6)2=36,
解得:x1=0,x2=
 ,
,∴ON=
 ,
,PN=2x-6=
 ,
,∴PM=6-PN=
 ,
,易证△DPM∽△PON,
∴
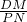 =
=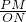 ,
,即
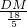 =
=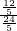 ,
,∴DM=
 ,
,∴CD=CM-DM=ON-DM=

 =3,
=3,∴D(3,6).
分析:(1)根据题意得出四边形OPDC为正方形,求出CD=OC=6,BD=3,即可证出tan∠DAB的值;
(2)根据OD⊥AC,得出∠COD=∠ACB,△OCD∽△CBA,即可求出CD的值,从而得出D点的坐标;
(3)先过点P作OA与N,再设P(x,2x-6),在Rt△OPN中,根据x2+(2x-6)2=36,解出x的值,从而得出PM的值,再证明△DPM∽△PON,得出
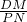 =
=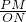 ,求出DM=
,求出DM= ,所以CD=CM-DM,从而求出D点的坐标.
,所以CD=CM-DM,从而求出D点的坐标.点评:此题考查了相似三角形的判定与性质;解题的关键是根据锐角三角函数的定义和相似三角形的判定与性质进行解答,特别注意P点的位置.

练习册系列答案
相关题目

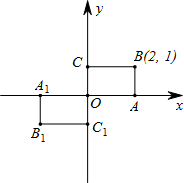 13、如图,矩形OABC的顶点O为坐标原点,点A在x轴上,点B的坐标为(2,1).如果将矩形0ABC绕点O旋转180°旋转后的图形为矩形OA1B1C1,那么点B1的坐标为( )
13、如图,矩形OABC的顶点O为坐标原点,点A在x轴上,点B的坐标为(2,1).如果将矩形0ABC绕点O旋转180°旋转后的图形为矩形OA1B1C1,那么点B1的坐标为( )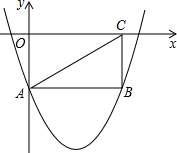 (2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
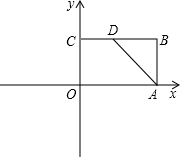 如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.
如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.