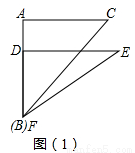
题目内容
将两块直角三角板按如图所示方式摆放，则△ABO与△CDO的面积比为1：3
1：3
．分析：设BC=a，则通过解直角三角形得到AB=a，CD=
a．利用“两角法”证得△ABO∽△CDO，则根据“相似三角形的面积之比等于相似比的平方”来填空．
| 3 |
解答：解：如图，设BC=a．
∵在直角△ABC中，∠A=∠BCA=45°，∴AB=BC=a．
∵在直角△BCD中，∠D=30°，∴CD=
a．
∵∠BCA=45°，∴∠DCO=90°-∠BCA=45°，
∴∠A=∠DCO．
又∵∠AOB=∠COD，
∴△ABO∽△CDO，
∴
=(
)2=
=
．
故答案是：1：3．
∵在直角△ABC中，∠A=∠BCA=45°，∴AB=BC=a．
∵在直角△BCD中，∠D=30°，∴CD=
| 3 |
∵∠BCA=45°，∴∠DCO=90°-∠BCA=45°，
∴∠A=∠DCO．
又∵∠AOB=∠COD，
∴△ABO∽△CDO，
∴
| S△ABO |
| S△CDO |
| AB |
| CD |
| a2 |
| 3a2 |
| 1 |
| 3 |
故答案是：1：3．
点评：本题考查了解直角三角形，相似三角形的判定与性质．三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边、对顶角等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．
练习册系列答案
相关题目
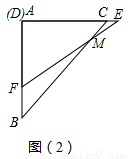
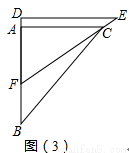
．将这副直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．
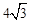。将这副直角三角板按如图（1）所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上，现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动。
