题目内容
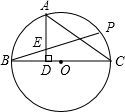 如图,已知BC是⊙O的直径,P是⊙O上一点,A是
如图,已知BC是⊙O的直径,P是⊙O上一点,A是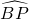 的中点,AD⊥BC于点D,BP与AD相交于点E.
的中点,AD⊥BC于点D,BP与AD相交于点E.
(1)当BC=6且∠ABC=60°时,求 的长;
的长;
(2)求证:AE=BE.
(3)过A点作AM∥BP,求证:AM是⊙O的切线.
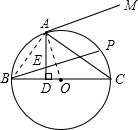 (1)解:连接OA,AB,
(1)解:连接OA,AB,∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠ABC=60°,
∵∠ACB=30°,
∴∠AOB=60°,
又∵OB=
 BC=
BC= ×6=3,
×6=3,∴AB弧的长为:l=
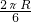 =
=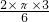 =π;
=π;(2)证明:∵点A是
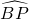 的中点,
的中点,∴
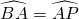 ,
,∴∠C=∠ABP.
∵BC为⊙O的直径,
∴∠BAC=90°,
即∠BAD+∠CAD=90°.
又∵AD⊥BC,
∴∠ADC=90°,
∴∠BAD=∠C,
∴∠ABP=∠BAD,
∴AE=BE;
(3)证明:∵A是
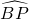 的中点,
的中点,∴AO⊥BP,
∵AM∥BP,
∴AM⊥AO,
即AM是⊙O的切线.
分析:(1)首先连接OA,AB,由BC是⊙O的直径,根据直径所对的圆周角是直角,即可得△ABC是直角三角形,又由BC=6,∠ABC=60°,即可求得⊙O的半径OB的长,继而求得
 的长;
的长;(2)由A是
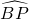 的中点,即可求得
的中点,即可求得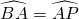 ,又由在同圆或等圆中,同弧所对的圆周角相等,即可得∠ABP=∠ACB,又由∠BAC=90°,AD⊥BC,易证得∠BAD=∠C,则问题得证;
,又由在同圆或等圆中,同弧所对的圆周角相等,即可得∠ABP=∠ACB,又由∠BAC=90°,AD⊥BC,易证得∠BAD=∠C,则问题得证;(3)由A是
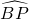 的中点,由垂径定理的知识,即可求得OA⊥BP,又由AM∥BP,即可证得AM是⊙O的切线.
的中点,由垂径定理的知识,即可求得OA⊥BP,又由AM∥BP,即可证得AM是⊙O的切线.点评:此题考查了圆的切线的判定,垂径定理,圆周角的性质以及直角三角形的性质等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 7、如图,已知BC是⊙O的直径,AD切⊙O于A,若∠C=40°,则∠DAC=( )
7、如图,已知BC是⊙O的直径,AD切⊙O于A,若∠C=40°,则∠DAC=( )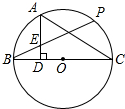 如图,已知BC是⊙O的直径,P是⊙O上一点,A是
如图,已知BC是⊙O的直径,P是⊙O上一点,A是
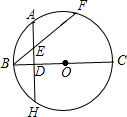 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为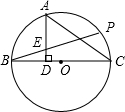 如图,已知BC是⊙O的直径,P是⊙O上一点,A是
如图,已知BC是⊙O的直径,P是⊙O上一点,A是 (2013•宁德质检)如图,已知BC是⊙O的直径,AB是⊙O的切线,AO交⊙O于点D,∠A=28°,则∠C=
(2013•宁德质检)如图,已知BC是⊙O的直径,AB是⊙O的切线,AO交⊙O于点D,∠A=28°,则∠C=