题目内容
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,⊙O是△ABC的内切圆,点D是斜边AB的中点,则tan∠ODA=________.

2.
【解析】
试题分析:连接OE、OF、OQ,设⊙O的半径为r,由勾股定理得AB=5,根据△ABC的内切圆,得到OE⊥AC,OF⊥BC,OE=OF,得到四边形CFOE是正方形,得到CE=CF=OF=OE,根据3-r+4-r=5求出r=1,AQ=AE=2,OQ=1,进而求出AD= ,DQ=AD-AQ=
,DQ=AD-AQ= ,所以
,所以 .
.
故答案为:2.

考点:三角形的内切圆与内心;勾股定理;正方形的判定和性质;切线长定理.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
(本题7分)今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的两种统计图表.

对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)请补全图中所示数的条形统计图;
(3)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”等级中的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,记下数字后放回袋中,另一人再从袋中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
 与
与 的交点在第一象限,则
的交点在第一象限,则 的取值可以是( )
的取值可以是( )
 .
.
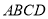 的边长为4,将其沿
的边长为4,将其沿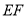 折叠,则图中①②③④四个三角形的周长之和为 .
折叠,则图中①②③④四个三角形的周长之和为 .