题目内容
【题目】(知识回顾)我们学习完《直角三角形的边角关系》之后知道,在![]() 中,当锐角
中,当锐角![]() 确定时,锐角
确定时,锐角![]() 的三角函数值也随之确定.结合课本所学知识,请你填空:
的三角函数值也随之确定.结合课本所学知识,请你填空:![]() ______;
______;![]() ______;
______;![]() ______.
______.
(深入探究)定义:在![]() 中,
中,![]() ,我们把
,我们把![]() 的对边与
的对边与![]() 的对边的比叫做
的对边的比叫做![]() 的邻弦,记作
的邻弦,记作![]() ,即:
,即:![]() .请解答下列问题:已知:在
.请解答下列问题:已知:在![]() 中,
中,![]() .
.
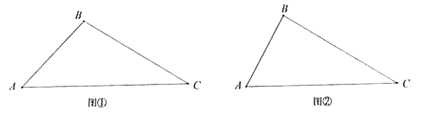
(1)如图①,若![]() ,求
,求![]() 的值;
的值;
(2)如图②,若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 是锐角,请你直接写出
是锐角,请你直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】知识回顾: ![]() ;
;![]() ;
;![]() ;深入探究:(1)
;深入探究:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
知识回顾:根据锐角三角函数的定义回答即可;
深入探究:(1)根据已知找到BC和AB的关系,依据定义计算出答案即可;
(2) 过点B向AC所在直线作垂线,根据thi A=![]() =
=![]() ,利用正弦首先表示出垂线段的长度,再根据正弦分两种情况:当∠A为锐角或钝角时,可得∠A=60°或120°.
,利用正弦首先表示出垂线段的长度,再根据正弦分两种情况:当∠A为锐角或钝角时,可得∠A=60°或120°.
(3) 根据题意,由thiA=![]() , sinA=
, sinA=![]() , sinC=
, sinC=![]() =
=![]() 易得BC=2BD,进而可得答案.
易得BC=2BD,进而可得答案.
解:【知识回顾】
![]() ;
;![]() ;
;![]() .
.
【深入探究】
(1)作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.

(3)作![]() 于点
于点![]() ,
,

在Rt△ABC中,thiA=![]() .
.
在Rt△BDA中,sinA=![]() .
.
在Rt△BDC中,sinC=![]() =
=![]() ,即BC=2BD.
,即BC=2BD.
∴thiA=2sinA.

练习册系列答案
相关题目