题目内容
8.已知a+b=$\sqrt{11}$,a-b=$\sqrt{7}$,求a2+b2+ab的值.分析 利用完全平方公式将已知变形,进而得出a2+b2=9,ab=1,进而得出答案.
解答 解:∵a+b=$\sqrt{11}$,
∴(a+b)2=a2+2ab+b2=11①,
∵a-b=$\sqrt{7}$,
∴(a-b)2=a2-2ab+b2=7②,
∴①+②得:2(a2+b2)=19,
则a2+b2=9,
①-②得:
4ab=4,
则ab=1,
故原式=9+1=10.
点评 此题主要考查了二次根式的化简求值以及完全平方公式的应用,熟练应用完全平方公式是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.已知点A表示的数为2,则到A点的距离为3表示的数为多少?( )
| A. | -1 | B. | 5 | C. | 3 | D. | -1或5 |
19.若am=5,an=3,则am+n的值为( )
| A. | 15 | B. | 25 | C. | 35 | D. | 45 |
13.若x=2是方程2a-3x=6的解,则a的值是( )
| A. | $\frac{1}{2}$ | B. | -4 | C. | $\frac{2}{3}$ | D. | 6 |
20.下列计算中正确的是( )
| A. | (-3x3y3)2=3x6y6 | B. | a10•a2=a20 | ||
| C. | (-m2)5•(-m3)2=m16 | D. | (-$\frac{1}{2}$x2y4)3=-$\frac{1}{8}$x6y12 |
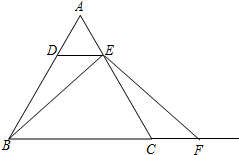 如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.