��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У���ACB=90����AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
��1����ֱ��MN�Ƶ�C��ת���ٵ�λ��ʱ����֤���١�ADC�ա�CEB����DE=AD+BE��
��2����ֱ��MN�Ƶ�C��ת���ڵ�λ��ʱ����֤��DE=AD��BE��
��3����ֱ��MN�Ƶ�C��ת���۵�λ��ʱ������DE��AD��BE����������������ϵ����ֱ��д�����������ϵ������Ҫ֤����

���𰸡���1����֤����������DE=CE+CD=AD+BE��2��֤����������3��DE=BE��AD����AD=BE��DE��BE=AD+DE�ȣ�
��������
(1���ɡ�ACB=90�㣬�á�ACD+��BCE=90�㣬��AD��MN��D��BE��MN��E�����ADC=��CEB=90�㣬���ݵȽǵ������ȵõ���ACD=��CBE���á�ADC�ա�CEB��
�ɡ�ADC�ա�CEB����AD=CE��DC=BE�����ɵõ�DE=DC+CE= AD+ BE��
��2���ɡ�ACB=90�㣬�á�ACD+��BCE=90�㣬��AD��MN��D��BE��MN��E�����ADC=��CEB=90�㣬���ݵȽǵ������ȵõ���ACD=��CBE���á�ADC�ա�CEB��
�ɡ�ADC�ա�CEB����AD=CE��DC=BE���ɵõ�DE =CE-CD=AD��BE
(3) �ɡ�ACB=90�㣬�á�ACD+��BCE=90�㣬��AD��MN��D��BE��MN��E�����ADC=��CEB=90�㣬���ݵȽǵ������ȵõ���ACD=��CBE���á�ADC�ա�CEB��
�ɡ�ADC�ա�CEB����AD=CE��DC=BE���ɵõ�DE =CD-CE=BE��AD��
��1����֤�����ߡ�ACB=90�㣬��ADC=90�㣬��BEC=90��
���ACD+��DAC=90�㣬��ACD+��BCE=90�㣬
���DAC=��BCE��
�ڡ�ADC���CEB�У�
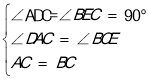 ��
��
���ADC�ա�CEB��AAS����
��DE=CE+CD=AD+BE���������£�
�ɢ�֪����ADC�ա�BEC��
��AD=CE��BE=CD��
��DE=CE+CD��
��DE=AD+BE��
��2��֤������AD��MN��D��BE��MN��E��
���ADC=��BEC=��ACB=90�㣬
���CAD+��ACD=90�㣬��ACD+��BCE=90�㣮
���CAD=��BCE��
�ڡ�ADC�͡�CEB�У�
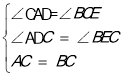 ��
��
���ADC�ա�CEB��AAS����
��CE=AD��CD=BE��
��DE=CE��CD=AD��BE��
��3���⣺ͬ��2������֤��ADC�ա�CEB��
��AD=CE��BE=CD
��CE=CD��ED
��AD=BE��ED����ED=BE��AD��
��MN��ת��ͼ3��λ��ʱ��AD��DE��BE������ĵ�����ϵ��DE=BE��AD����AD=BE��DE��BE=AD+DE�ȣ���

 ��У����ϵ�д�
��У����ϵ�д�


