题目内容
 如图,已知A(2,0),点P为y轴正半轴上的一个动点,分别以AO、OP为腰在第一、二象限作等腰Rt△APC和等腰Rt△OPD,连接CD交y轴于N点,当点P在y轴上移动时,求PN的长度.
如图,已知A(2,0),点P为y轴正半轴上的一个动点,分别以AO、OP为腰在第一、二象限作等腰Rt△APC和等腰Rt△OPD,连接CD交y轴于N点,当点P在y轴上移动时,求PN的长度.考点:平行四边形的判定与性质,坐标与图形性质,全等三角形的判定与性质
专题:
分析:首先过点C作CE⊥y轴于点E,连接DE,由别以AO、OP为腰在第一、二象限作等腰Rt△APC和等腰Rt△OPD,易证得△AOP≌△PEC(AAS),则可证得PE=OA=2,CE=OP,又可证得四边形PDEC是平行四边形,继而求得PN的长度.
解答:解:如图,过点C作CE⊥y轴于点E,连接DE,
则∠CEP=∠POA=90°,
∵△APC是等腰直角三角形,
∴AP=CP,∠APC=90°,
∴∠OPA+∠CPN=90°,
∵∠OPA+∠OAP=90°,
∴∠OAP=∠CPN,
在△AOP和△PEC中,
,
∴△AOP≌△PEC(AAS),
∴PE=OA=2,CE=OP,
∵△OPD是等腰直角三角形,
∴DP⊥y轴,PD=OP,
∴CE∥PD,CE=PD,
∴四边形PDEC是平行四边形,
∴PN=
PE=1.
则∠CEP=∠POA=90°,
∵△APC是等腰直角三角形,

∴AP=CP,∠APC=90°,
∴∠OPA+∠CPN=90°,
∵∠OPA+∠OAP=90°,
∴∠OAP=∠CPN,
在△AOP和△PEC中,
|
∴△AOP≌△PEC(AAS),
∴PE=OA=2,CE=OP,
∵△OPD是等腰直角三角形,
∴DP⊥y轴,PD=OP,
∴CE∥PD,CE=PD,
∴四边形PDEC是平行四边形,
∴PN=
| 1 |
| 2 |
点评:此题考查了平行四边形的判定与性质、全等三角形的判定与性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列各式变形正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法中,正确的是( )
| A、同一条弦所对的两条弧一定是等弧 |
| B、长度相等的两条弧是等弧 |
| C、正多边形一定是轴对称图形 |
| D、三角形的外心到三角形各边的距离相等 |
 如图,已知在△ABC中,AB=AC,∠B=70°,BD=CF,BE=DC.
如图,已知在△ABC中,AB=AC,∠B=70°,BD=CF,BE=DC.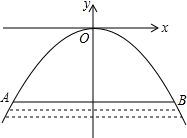 某涵洞是抛物线型,把它放到如图所示的坐标系中,它的表达式为y=-x2,此时测得水渠宽AB=8m.
某涵洞是抛物线型,把它放到如图所示的坐标系中,它的表达式为y=-x2,此时测得水渠宽AB=8m.