题目内容
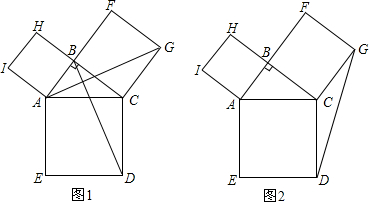
探索与研究:在△ABC中,∠ABC=90°,分别以边AB、BC、CA向△ABC外作正方形ABHI、正方形BCGF、正方形CAED,连接GD、AG、BD.
(1)如图甲,求证:AG=BD.
(2)如图乙,试说明:S△ABC=S△CDG.
(提示:正方形的四条边相等,四个角均为直角)
解:(1)∵四边形ABHI、四边形BCGF和四边形CAED都是正方形,
∴AB=BH=HI=AI,BC=CG=GF=BF,AE=DE=CD=AC,∠H=∠I=∠E=∠F=∠IAB=∠ABH=∠FBC=∠BCG=∠FGC=∠BAC=∠ACD=90°.
∴∠ACD+∠ACB=∠BCG+∠ACB,
∴∠DCB=∠ACG.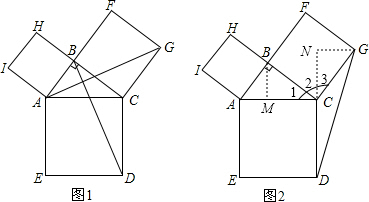
在△ACG和△DCB中,
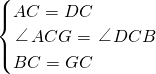 ,
,
∴△ACG≌△DCB(SAS),
∴AG=BD;
(2)如图2,作BM⊥AC于M,GN⊥DC的延长于点N.
∴∠BMC=∠N=90°
∵∠+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
在△BMC和△GNC中,
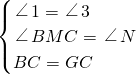 ,
,
∴△BMC≌△GNC(SAS),
∴BM=GN,
∴ AC•BM=
AC•BM= DC•GN,
DC•GN,
∵S△ABC= AC•BM,S△DCG=
AC•BM,S△DCG= DC•GN,
DC•GN,
∴S△ABC=S△CDG.
分析:(1)由正方形的性质就可以得出△ACG≌△DCB,就可以得出结论;
(2)延长DC交GF于H,证明△BMC≌△GNC,就可以得出BM=GN,就可以得出结论.
点评:本题考查了正方形的性质的运用,三角形全等的判定及性质的运用,三角形的面积公式的运用,在解答时证明三角形全等是关键.
∴AB=BH=HI=AI,BC=CG=GF=BF,AE=DE=CD=AC,∠H=∠I=∠E=∠F=∠IAB=∠ABH=∠FBC=∠BCG=∠FGC=∠BAC=∠ACD=90°.
∴∠ACD+∠ACB=∠BCG+∠ACB,
∴∠DCB=∠ACG.

在△ACG和△DCB中,
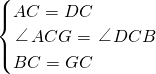 ,
,∴△ACG≌△DCB(SAS),
∴AG=BD;
(2)如图2,作BM⊥AC于M,GN⊥DC的延长于点N.
∴∠BMC=∠N=90°
∵∠+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
在△BMC和△GNC中,
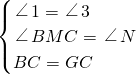 ,
,∴△BMC≌△GNC(SAS),
∴BM=GN,
∴
 AC•BM=
AC•BM= DC•GN,
DC•GN,∵S△ABC=
 AC•BM,S△DCG=
AC•BM,S△DCG= DC•GN,
DC•GN,∴S△ABC=S△CDG.
分析:(1)由正方形的性质就可以得出△ACG≌△DCB,就可以得出结论;
(2)延长DC交GF于H,证明△BMC≌△GNC,就可以得出BM=GN,就可以得出结论.
点评:本题考查了正方形的性质的运用,三角形全等的判定及性质的运用,三角形的面积公式的运用,在解答时证明三角形全等是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.