题目内容
7.解方程:(1)x2-2x=5;
(2)x2-3x-3=0;
(3)4(x+3)2=25(x-2)2.
分析 (1)利用完全平方公式配方,开方即可求出解.
(2)方程变形后,利用完全平方公式配方,开方即可求出解.
(3)移项后分解因式得出(7x-16)(-3x+4)=0,推出方程7x-16=0,-3x+4=0,求出方程的解即可.
解答 解:(1)x2-2x=5;
x2-2x+1=5+1,
(x-1)2=6,
∴x-1=$±\sqrt{6}$,
∴x1=1+$\sqrt{6}$,x2=1-$\sqrt{6}$;
(2)x2-3x-3=0;
x2-3x=3,
x2-3x+($\frac{3}{2}$)2=3+$\frac{9}{4}$,
(x-$\frac{3}{2}$)2=$\frac{21}{4}$,
x-$\frac{3}{2}$=±$\frac{\sqrt{21}}{2}$,
∴x1=$\frac{3+\sqrt{21}}{2}$,x2=$\frac{3-\sqrt{21}}{2}$;
(3)4(x+3)2=25(x-2)2.
4(x+3)2-25(x-2)2=0,
[2(x+3)+5(x-2)][2(x+3)-5(x-2)=0,
∴7x-4=0或-3x+16=0,
∴x1=$\frac{4}{7}$,x2=-$\frac{16}{3}$.
点评 本题考查了解一元二次方程,把一元二次方程转化为两个一元一次方程求解是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
17.正方形具有而矩形不具有的性质是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相垂直 |
17.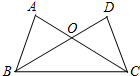 如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )
如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )
 如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )
如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | ∠ACB=∠DBC | C. | AB=DC | D. | AC=DB |
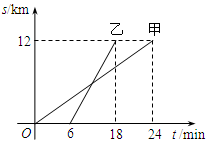 甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米.
甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米. 如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.
如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.