题目内容
1.已知一个正方体的体积是1000cm3,现在要在它的8个角上分别截去1个大小相同的小正方体,使截后余下的体积是488cm3,问截得的每个小正方体的棱长是多少?如果要将该正方体加大,加大后的体积是原来体积的8倍,新正方体的棱长应为多少呢?分析 根据有理数的减法、有理数的除法,可得小正方体的体积,根据开立方运算,可得小正方体的体积;
根据有理数的乘法,可得大正方体的体积,根据开立方运算,可得答案.
解答 解:8个小正方体的体积1000-488=512cm3,
1个小正方体的体积512÷8=64cm3,
截得的每个小正方体的棱长是$\root{3}{64}$=4cm;
大正方体的体积是8×1000=8000cm3,
截得的每个小正方体的棱长是$\root{3}{8000}$=20cm.
点评 本题考查了立方根,利用有理数的运算得出正方体的体积,再利用开立方运算求出棱长.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12.(1)填表:
(2)由上表找规律,并根据规律填空:
①已知:$\sqrt{49}$=7,则$\sqrt{0.49}$=0.7,$\sqrt{490000}$=700
②已知:$\sqrt{529}$=23,则$\sqrt{0.0529}$=0.23,$\sqrt{52900}$=230.
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知:$\sqrt{49}$=7,则$\sqrt{0.49}$=0.7,$\sqrt{490000}$=700
②已知:$\sqrt{529}$=23,则$\sqrt{0.0529}$=0.23,$\sqrt{52900}$=230.
9.若α、β是一元二次方程x2+3x-7=0的两根,则α2+β2=( )
| A. | -7 | B. | 32 | C. | 23 | D. | 14 |
6.股市有风险,入市须谨慎,股民小李考虑再三后在上星期五买进某公司股票1000股,每股27元,下表为每周内每日该股票的涨跌(单位:元)情况.
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价为多少元?每股最低价为多少元?
(3)已知小李股民买进股票时付了1.5‰的手续费,卖出时还需付成交额1.5‰的手续费和1‰的交易锐,如果小李在星期五收盘前将全部卖出股票,他的收益如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内每股最高价为多少元?每股最低价为多少元?
(3)已知小李股民买进股票时付了1.5‰的手续费,卖出时还需付成交额1.5‰的手续费和1‰的交易锐,如果小李在星期五收盘前将全部卖出股票,他的收益如何?
10.下列计算中,正确的是( )
| A. | a•a=2a | B. | (2a)3=6a3 | C. | a+2a=3a2 | D. | a6÷a4=a2 |
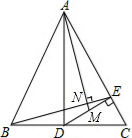 已知,如图所示,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M是DE的中点,BE与AM交于点N.求证:∠EBC=∠DAM.
已知,如图所示,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M是DE的中点,BE与AM交于点N.求证:∠EBC=∠DAM.