题目内容
（10分）如图，O是坐标原点，直线OA与双曲线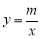
在第一象限内交于点A，过点A的直线
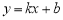与x轴正半轴交于点B，与双曲线的另一交点为C，连结OC. 若
，
.
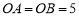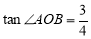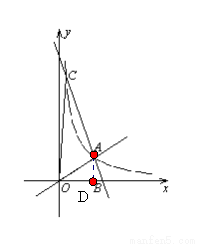
（1）求双曲线和直线AB的解析式；
（2）求△AOC的面积.
（3）在第一象限内，根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
（1）双曲线的解析式为
，直线AB的解析式为
；（2）
；（3）
．
【解析】
试题分析：（1）由
，
.可求出A点的坐标带入
即可求出双曲线，再把A、B的坐标带入直线可确定直线AB的解析式；
（2）先求出C点的坐标，就可以求出△OCB和△OAB的面积，△AOC的面积=△OCB的面积-△OAB的面积.
（3）根据图像观察即可.
试题解析：（1）过A作AD⊥OB，垂足为D 在Rt△AOD中，，
可得
设OD=4x，AD=3x，由勾股定理的：OA=5x=5解得x=1，∴OD=4,，AD=3
∴A、B两点的坐标分别为（4,3）（5,0）
把A（4,3）带入得k=4
3=12 ∴ 双曲线的解析式为；
A、B两点（4,3）（5,0）带入
得：
和
，
解得
∴直线AB的解析式为
（2）解
=
得
当x=1时，y=12
∴
,
∴
-
=
（3）观察图像可知时一次函数的值大于反比例函数的值
考点：求一次函数、反比例函数的解析式，函数与三角形的应用.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的值是3，则代数式
的值是 ．
的图象上的两个交点．
与反比例函数
的图象交于点A（2，1），B（-1，-2），则使
的
的取值范围是 ．
是反比例函数，则m ．
，再求当x满足
时，此分式的值.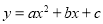 
的部分对应值如下表：
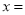1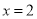 
对应的函数值
-8 
B．
D．