题目内容
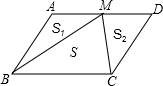 如图所示,M是?ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列S,S1,S2的大小关系中正确的是
如图所示,M是?ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列S,S1,S2的大小关系中正确的是
- A.S>S1+S2
- B.S=S1+S2
- C.S<S1+S2
- D.S与S1+S2的大小关系无法确定
B
分析:根据平行四边形的性质得到AD=BC,而△CMB的面积为S= BC•高,△CDM的面积为S1=
BC•高,△CDM的面积为S1= MD•高,△ABM的面积为S2=
MD•高,△ABM的面积为S2= AM•高,这样得到S1+S2=
AM•高,这样得到S1+S2= MD•高+
MD•高+ AM•高=
AM•高= (MD+AM)•高=
(MD+AM)•高= BC•高=S,由此则可以推出S,S1,S2的大小关系.
BC•高=S,由此则可以推出S,S1,S2的大小关系.
解答:∵四边形ABCD是平行四边形,
∴AD=BC,
∵△CMB的面积为S= BC•高,△CDM的面积为S1=
BC•高,△CDM的面积为S1= MD•高,△ABM的面积为S2=
MD•高,△ABM的面积为S2= AM•高,
AM•高,
而它们的高都是等于平行四边形的高,
∴S1+S2= MD•高+
MD•高+ AM•高=
AM•高= (MD+AM)•高=
(MD+AM)•高= AD•高=
AD•高= BC•高=S,
BC•高=S,
则S,S1,S2的大小关系是S=S1+S2.
故选B.
点评:本题考查平行四边形的性质对边相等以及三角形的面积计算公式.
分析:根据平行四边形的性质得到AD=BC,而△CMB的面积为S=
 BC•高,△CDM的面积为S1=
BC•高,△CDM的面积为S1= MD•高,△ABM的面积为S2=
MD•高,△ABM的面积为S2= AM•高,这样得到S1+S2=
AM•高,这样得到S1+S2= MD•高+
MD•高+ AM•高=
AM•高= (MD+AM)•高=
(MD+AM)•高= BC•高=S,由此则可以推出S,S1,S2的大小关系.
BC•高=S,由此则可以推出S,S1,S2的大小关系.解答:∵四边形ABCD是平行四边形,
∴AD=BC,
∵△CMB的面积为S=
 BC•高,△CDM的面积为S1=
BC•高,△CDM的面积为S1= MD•高,△ABM的面积为S2=
MD•高,△ABM的面积为S2= AM•高,
AM•高,而它们的高都是等于平行四边形的高,
∴S1+S2=
 MD•高+
MD•高+ AM•高=
AM•高= (MD+AM)•高=
(MD+AM)•高= AD•高=
AD•高= BC•高=S,
BC•高=S,则S,S1,S2的大小关系是S=S1+S2.
故选B.
点评:本题考查平行四边形的性质对边相等以及三角形的面积计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 23、如图所示,CD是AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( )
23、如图所示,CD是AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( ) 12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C
12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C 4、已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.求证:∠ABC=2∠C.
4、已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.求证:∠ABC=2∠C. 如图所示,CD是AB的垂直平分线,若AC=10cm,BD=20cm,则四边形ACBD的周长为
如图所示,CD是AB的垂直平分线,若AC=10cm,BD=20cm,则四边形ACBD的周长为 如图所示,CD是AB的垂直平分线,若AC=2cm,BD=3cm,则四边形ACBD的周长是
如图所示,CD是AB的垂直平分线,若AC=2cm,BD=3cm,则四边形ACBD的周长是