题目内容
【题目】如图，在边长为1的小正方形组成的网格中，四边形ABCD的四个顶点都在格点上，请按要求完成下列各题．
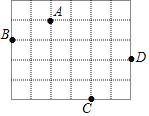
（1）线段AB的长为__，BC的长为__，CD的长为__，AD的长为__；
（2）连接AC，通过计算△ACD的形状是__；△ABC的形状是__．
【答案】（1）
，5，2
，2；（2）等腰三角形，直角三角形
【解析】
（1）利用勾股定理计算即可． （2）根据等腰三角形的定义，勾股定理的逆定理判断即可．
解：（1）由题意AB＝
BC
CD
AD
故答案为，5，2，2
（2）∵AC
∴AC＝AD，
∴△ACD是等腰三角形，
∵AB＝，AC＝
，BC＝5，
∴AB2+AC2＝25＝BC2，
∴∠BAC＝90°
∴△ABC是直角三角形，
故答案为等腰三角形，直角三角形．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
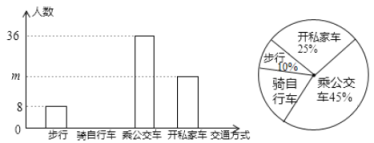
【题目】《中国汉字听写大会》 唤醒了很多人对文字基本功的重视和对汉字文化的学习，某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中200名学生的海选比赛成绩（成绩
取整数，总分100分）作为样本进行整理，得到下列统计图表：
抽取的200名学生海选成绩分组表
组别 | 海选成绩 |
A组 |
|
B组 |
|
C组 |
|
D组 |
|
E组 |
|
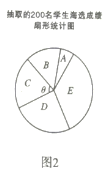
请根据所给信息，解答下列问题
（1）请把图1中的条形统计图补充完整；
（2）在图2的扇形统计图中，表示
组扇形的圆心角
的度数为_______度；
（3）规定海选成绩在90分以上（包括90分）记为“优等”，请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人；
（4）经过统计发现，在
组中，有2位男生和2位女生获得了满分，如果从这4人中挑选2人代表学校参加比赛，请用树状图或列表法求出所选两人正好是一男一女的概率是多少？
