Question

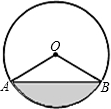如图，AB是⊙O的弦，OA=2，∠AOB=120°，则图中阴影部分的面积为________．（结果保留根号和π ）

Answer 1

-．
分析：过O作OC⊥AB于C，根据垂径定理得到AC=BC；而∠AOB=120°，OA=OB，根据等腰三角形的性质得∠A=30°；在Rt△OAC中，OA=2，∠A=30°，根据含30度的直角三角形三边的关系得到OC和AC，则可求出AB，最后根据扇形的面积公式和三角形的面积公式利用S_阴影部分=S_扇形OAB-S_△OAB进行计算即可．
解答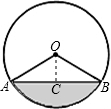：解：过O作OC⊥AB于C，如图，
∴AC=BC，
而∠AOB=120°，OA=OB，
∴∠A=（180°-120°）=30°，
在Rt△OAC中，OA=2，∠A=30°，
∴OC=1，AC=，
∴AB=2，
∴S_阴影部分=S_扇形OAB-S_△OAB
=-•1•2
=-．
故答案为-．
点评：本题考查了扇形的面积公式：S=；也考查了垂径定理和等腰三角形的性质以及含30度的直角三角形三边的关系．