Question

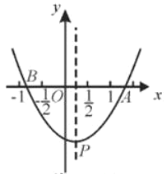
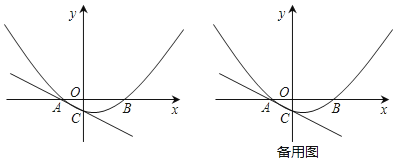
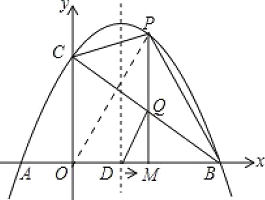
【题目】如图，已知抛物线 y x2 bx c 的图象与 x 轴交于 A1, 0 、 B 4, 0 两点， 与 y 轴交于点C ，抛物线的对称轴与 x 轴交于点 D ，点 M 从O 点出发，以每秒 1 个单位长度的速度向 B 点运动（运动到 B 点停止），过点 M 作 x 轴的垂线，交抛物线于点 P ，交 BC 与点Q .

（1）求抛物线的解析式；

（2）设当点 M 运动了t （秒）时，四边形OBPC 的面积为 S ，求 S 与t 的函数关系式，并指出自变量t 的取值范围；

（3）在线段 BC 上是否存在点Q ，使得DBQ 成为等腰三角形？若存在，求出点Q 的坐标；若不存在，说明理由.

Answer 1

【答案】（1）抛物线的解析式为y x2 3x 4.（2）S＝2x2＋8x＋8（0≤x≤4）

（3）存在，Q的坐标为（，）, 或（4,）, 或（,）.

【解析】

（1）把A1, 0 、 B 4, 0 两点代入解析式即可求解；

（2）设点P的坐标为P（x，y），由S四边形OBPC＝S△OPC＋S△OPB可列出S与x的函数关系式，由于B（4，0），所以0≤x≤4；

（3）有三种可能：①BQ＝DQ，②BQ＝BD＝，③DQ＝BD＝，分别讨论即可求得．

解：（1）把A1, 0 、 B 4, 0 两点代入解析式得

，解得

∴抛物线的解析式为y x2 3x 4.

∴C点坐标为（0,4）

设BC的解析式为y=kx+b，利用B 4, 0，C（0,4）得到BC的解析式为y=-x+4.

（2）如图，连接OP，设点P的坐标为P（x，y）

S四边形OBPC＝S△OPC＋S△OPB＝×4×x＋×4×y

＝2x＋2y

＝2x＋2（x2＋3x＋4）

＝2x2＋8x＋8．

∵点M运动到B点上停止，

∴0≤x≤4

∴S＝2x2＋8x＋8（0≤x≤4）

（3）存在．

∵y＝x2＋3x＋4＝（x）2＋

∴顶点的坐标为（，），

∵OB＝OC＝4，

∴BC＝，∠ABC＝45°，

故①若BQ＝DQ

∵BQ＝DQ，BD＝4=

∴BM＝QM＝，

∴OM＝4=

所以Q的坐标为Q（，）

②若BQ＝BD＝

∵∠QBM=∠CBO，∠BMQ=∠BOC=90°

∴△BQM∽△BCO，

∴，

∴

∴QM＝BM＝

∴OM＝4

所以Q的坐标为Q（4,）．

③若DQ＝BD＝

∵∠ABC＝45°，

∴DQ⊥BD，

∴△DBQ是等腰直角三角形，

∴DQ＝BD＝

所以Q的坐标为Q（,），

综上所述，Q的坐标为Q（，）, 或（4,）, 或（,）.