题目内容
 如图已知:线段AB上有一点D,且C为线段DB的中点,点D分线段AC为1:3,若CD=9cm,则AB等于多少厘米?
如图已知:线段AB上有一点D,且C为线段DB的中点,点D分线段AC为1:3,若CD=9cm,则AB等于多少厘米?分析:由已知条件可知,且C为线段DB的中点,DC=BC=
DB,又因为点D分线段AC为1:3,则DC=3AD,AD=
CD,故AB=AD+BD=2DC+
CD,由此代入数据求得答案.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵C为线段DB的中点,
∴DC=BC=
DB,
∵点D分线段AC为1:3,
∴DC=3AD,AD=
CD,
∴AB=AD+BD=2DC+
CD=2×9+9×
=21cm.
∴DC=BC=
| 1 |
| 2 |
∵点D分线段AC为1:3,
∴DC=3AD,AD=
| 1 |
| 3 |
∴AB=AD+BD=2DC+
| 1 |
| 3 |
| 1 |
| 3 |
点评:结合图形解题直观形象,从图中很容易能看出各线段之间的关系.利用中点性质转化线段之间的倍数关系是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
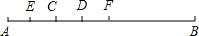 如图,C是线段AB上一点,D、E、F分别是线段AB、线段AC、线段BC的中点,已知AC=18cm.求DF.
如图,C是线段AB上一点,D、E、F分别是线段AB、线段AC、线段BC的中点,已知AC=18cm.求DF.
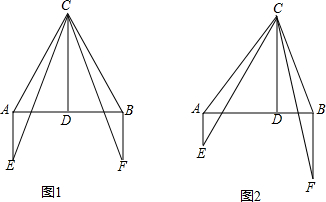
 如图已知:线段AB上有一点D,且C为线段DB的中点,点D分线段AC为1:3,若CD=9cm,则AB等于多少厘米?
如图已知:线段AB上有一点D,且C为线段DB的中点,点D分线段AC为1:3,若CD=9cm,则AB等于多少厘米?