题目内容
 一只船以每小时a海里的速度由点A向正北方向航行,开始航行时,从A点观测灯塔C在北偏东α的方向,经过t小时后,船在B点,此时C点在B的北偏东β的方向上,求A到C的距离.
一只船以每小时a海里的速度由点A向正北方向航行,开始航行时,从A点观测灯塔C在北偏东α的方向,经过t小时后,船在B点,此时C点在B的北偏东β的方向上,求A到C的距离.
解:在Rt△ACD中,AD=CD•cotα,
在Rt△ACD中,BD=CD•cotβ,
∴AB=AD-BD=CD(cotα-cotβ);
而AB=at海里,
即at=CD(cotα-cotβ),
∴ ;
;
在Rt△ACD中, ,
,
∴ (海里).
(海里).
分析:本题中CD是公共直角边,可用CD表示出AD和BD,再根据AB的值(路程=速度×时间),求出CD,在直角△ACD中,利用三角函数即可求得AC的长.
点评:两个直角三角形有公共的直角边,先求出公共边是解决此类题目的基本出发点.正确理解解直角三角形的条件是解题关键.
在Rt△ACD中,BD=CD•cotβ,
∴AB=AD-BD=CD(cotα-cotβ);
而AB=at海里,
即at=CD(cotα-cotβ),
∴
 ;
;在Rt△ACD中,
 ,
,∴
 (海里).
(海里).分析:本题中CD是公共直角边,可用CD表示出AD和BD,再根据AB的值(路程=速度×时间),求出CD,在直角△ACD中,利用三角函数即可求得AC的长.
点评:两个直角三角形有公共的直角边,先求出公共边是解决此类题目的基本出发点.正确理解解直角三角形的条件是解题关键.

练习册系列答案
相关题目
 一只船以每小时a海里的速度由点A向正北方向航行,开始航行时,从A点观测灯塔C在北偏东α的方向,经过t小时后,船在B点,此时C点在B的北偏东β的方向上,求A到C的距离.
一只船以每小时a海里的速度由点A向正北方向航行,开始航行时,从A点观测灯塔C在北偏东α的方向,经过t小时后,船在B点,此时C点在B的北偏东β的方向上,求A到C的距离.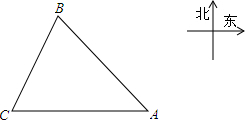 (1998•四川)一船在A处观测到西北方向有一座灯塔B,这只船沿正西方向以每小时25海里的速度航行1小时12分钟后到达C处,这时测得灯塔B在北偏东26°方向.求灯塔B到C处的距离(结果用含锐角三角函数的式子表示).
(1998•四川)一船在A处观测到西北方向有一座灯塔B,这只船沿正西方向以每小时25海里的速度航行1小时12分钟后到达C处,这时测得灯塔B在北偏东26°方向.求灯塔B到C处的距离(结果用含锐角三角函数的式子表示). 一船在A处观测到西北方向有一座灯塔B,这只船沿正西方向以每小时25海里的速度航行1小时12分钟后到达C处,这时测得灯塔B在北偏东26°方向.求灯塔B到C处的距离(结果用含锐角三角函数的式子表示).
一船在A处观测到西北方向有一座灯塔B,这只船沿正西方向以每小时25海里的速度航行1小时12分钟后到达C处,这时测得灯塔B在北偏东26°方向.求灯塔B到C处的距离(结果用含锐角三角函数的式子表示).