题目内容
三角形ABC中，AB=10，AC=17，BC边上的高线AD=8．则BC=________．
9或21
分析：由勾股定理可分别在Rt△ABD和Rt△ADC中求出BD、DC的长，然后分两种情况考虑：
①D点在线段BC上，②D点在CB的延长线上；根据D点的不同位置可得BD、DC、BC三条线段不同的数量关系，从而得到BC的值．
解答：
解：Rt△ACD中，AC=17，AD=8，由勾股定理得：CD=
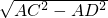=15；
Rt△ABD中，AB=10，AD=8，由勾股定理得：BD=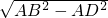
=6；
①点D在线段BC上时，BC=BD+CD=21，
②点D在CB的延长线上时，BC=CD-BD=9，
故BC的长为9或21．
点评：此题主要考查的是勾股定理的应用，应注意的是点D的位置有两种情况，要分类讨论，不要漏解．
分析：由勾股定理可分别在Rt△ABD和Rt△ADC中求出BD、DC的长，然后分两种情况考虑：
①D点在线段BC上，②D点在CB的延长线上；根据D点的不同位置可得BD、DC、BC三条线段不同的数量关系，从而得到BC的值．
解答：
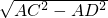解：Rt△ACD中，AC=17，AD=8，由勾股定理得：CD==15；Rt△ABD中，AB=10，AD=8，由勾股定理得：BD=
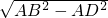=6；①点D在线段BC上时，BC=BD+CD=21，
②点D在CB的延长线上时，BC=CD-BD=9，
故BC的长为9或21．
点评：此题主要考查的是勾股定理的应用，应注意的是点D的位置有两种情况，要分类讨论，不要漏解．
练习册系列答案
相关题目
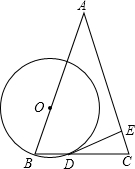如图，在等腰三角形ABC中，AB=AC，O为AB上一点，以O为圆心、OB长为半径的圆交BC于D，DE⊥AC交AC于E．
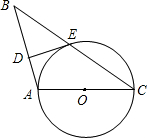为点D，
1、在锐角三角形ABC中，AB＞AC，AM为中线，P为△AMC内一点，证明：PB＞PC（如图）．
如图等腰三角形ABC中，AB=AC=3，BC=2