Question

在矩形ABCD中，AB=3，点P在对角线AC上，直线l过点P，且与AC垂直交AD边于点E．
（1）如图1，若直线l过点B，把△ABE沿直线l翻折，点A与矩形ABCD的对称中心O重合，求BC的长；
（2）如图2，若直线l与AB相交于点F且AP=

1

4

AC，设AD的长为x，五边形BCDEF的面积为S，
①求S关于x的函数关系式，并写出自变量x的取值范围；
②探索：是否存在这样的x，使得以A为圆心，以x-

3

4

长为半径的圆与直线l相切？若存在，请求出x的值若不存在，请说明理由．

Answer 1

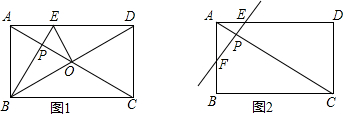
分析：（1）利用直角三角形斜边上的中线等于斜边的一半以及轴对称的性质得到AC=2AB，进而利用勾股定理求解即可．
（2）①五边形的面积=矩形的面积-S_△AEF，利用相似可求得AE，AF的长度．
②圆与直线l相切，半径x-

3

4

应等于AO长．

解答：解：（1）∵O是矩形ABCD的对称中心，
∴OB=AO=

1

2

AC（1分）
又∵AB=OB，AB=3，
AC=6，（1分）
在Rt△ABC中BC²=AC²-AB²
∴BC=3

3

．（2分）

（2）①在Rt△ADC中
∵AD=x，AB=3，
∴AC=

x2+9

．（1分）
∵AP=

1

4

x2+9

（1分）
易证△APF∽△ABC，

AP

AB

=

AF

AC

，
AF=

1

12

(x2+9)，（1分）
同理可得 AE=

x2+9

4x

，（1分）
∴S△AEF=

1

2

AE•AF=

(x2+9)2

96x

，
∴S=3x-

(x2+9)2

96x

，
即：S=

-x4+270x2-81

96x

（

3

＜x＜3

3

）．
②若圆A与直线l相切，
则 x-

3

4

=

1

4

x2+9

，（1分）
15x²-24x=0，x₁=0（舍去），x2=

8

5

．（1分）
∵x2=

8

5

＜

3

，
∴不存在这样的x，使圆A与直线l相切．（1分）

点评：本题考查了翻折变换的知识，同时涉及了矩形和切线的性质，注意掌握直角三角形斜边上的中线等于斜边的一半；圆与直线相切，半径等于圆心到直线的距离．