题目内容
【题目】在一空旷场地上设计一落地为矩形
的小屋，
，拴住小狗的
长的绳子一端固定在
点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为
.
（1）如图1，若
，则
__________
.
（2）如图2，现考虑在（1）中的矩形小屋的右侧以
为边拓展一正
区域，使之变成落地为五边形
的小屋，其他条件不变，则在
的变化过程中，当
取得最小值时，求边的长及的最小值.
【答案】（1）88π；（2）BC长为
；S的最小值为
．
【解析】
（1）小狗活动的区域面积为以B为圆心、10为半径的
圆，以C为圆心、6为半径的
圆和以A为圆心、4为半径的圆的面积和，据此列式求解可得；
（2）此时小狗活动的区域面积为以B为圆心、10为半径的圆，以A为圆心、x为半径的圆、以C为圆心、10-x为半径的
圆的面积和，列出函数解析式，由二次函数的性质解答即可．
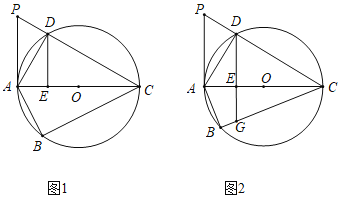
解：（1）如图1，拴住小狗的10m长的绳子一端固定在B点处，小狗可以活动的区域如图所示：
由图可知，小狗活动的区域面积为以B为圆心、10为半径的圆，以C为圆心、6为半径的圆和以A为圆心、4为半径的圆的面积和，
∴S=×π102+π62+π42=88π，
故答案为：88π；
（2）如图2，
设BC=x，则AB=10-x，
∴S=π102+πx2+π（10-x）2
=
（x2-5x+250）
=（x-
）2+，
当x=时，S取得最小值，
∴BC长为；S的最小值为．
优等生题库系列答案
【题目】近年来，“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注，为此，某校随机调查了n名学生对此问题的看法（看法分为三种：没有影响，影响不大，影响很大），并将调查结果 绘制成如下不完整的统计表和扇形统计图，根据统计图表提供的信息，解答下列问题：
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数（人） | 40 | 60 | m |
（1）求n的值；
（2）统计表中的m= ；
（3）估计该校1800名学生中认为“影响很大”的学生人数．
