题目内容

如图，反比例函数y= $数学公式$ 的图象经过点A（- $数学公式$ ，b），过点A作AB⊥x轴于点B，△AOB的面积为 $数学公式$ ．
（1）求k和b的值．
（2）若一次函数y=ax+1的图象经过点A，并且与x轴相交于点M，与反比例函数的图象交于另一点C（ $数学公式$ ，-1）．
①求AO：AM的值．
②求方程ax+1- $数学公式$ =0的解（请直接写出答案）
③求不等式ax+1- $数学公式$ ＜0的解集（请直接写出答案）

解：（1）∵AB⊥BD，A（- $\text{[math]}$ ，b），
∴S_△AOB= $\text{[math]}$ AB•BO= $\text{[math]}$ ，
即 $\text{[math]}$ b•|- $\text{[math]}$ |= $\text{[math]}$ ，
解得：b=2，
又∵点A在双曲线y= $\text{[math]}$ 上，
∴k=2×（- $\text{[math]}$ ）=-2 $\text{[math]}$ ；

（2）①∵A（- $\text{[math]}$ ，2），在直线y=ax+1上
∴2=- $\text{[math]}$ a+1　解得：a=- $\text{[math]}$
∴y=- $\text{[math]}$ x+1，
当y=0时，x= $\text{[math]}$ ，
∴M（ $\text{[math]}$ ，0），
∴AO= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
AM= $\text{[math]}$ = $\text{[math]}$ =4，
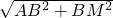∴AO：AM= $\text{[math]}$ ：4，

②∵求方程ax+1- $\text{[math]}$ =0的解，即为求y=ax+1，与y= $\text{[math]}$ 图象交点横坐标，根据A，C坐标得出，
∴方程ax+1- $\text{[math]}$ =0的解为：x₁=- $\text{[math]}$ ，x₂=2 $\text{[math]}$ ；

③∵由ax+1- $\text{[math]}$ ＜0，得出ax+1＜ $\text{[math]}$ ，即反比例函数大于一次函数，
∴不等式ax+1- $\text{[math]}$ ＜0的解集为：- $\text{[math]}$ ＜x＜0或 x＞2 $\text{[math]}$ ．
分析：（1）根据点A（- $\text{[math]}$ ，b）知OB= $\text{[math]}$ ，由△AOB的面积为 $\text{[math]}$ 求出b，再由A点坐标求出k；
（2）①由一次函数y=ax+1的图象经过点A求出a，得函数解析式，再求M的坐标，得BM的长；在△AOB中求OA的长，最后求比值，
②根据ax+1= $\text{[math]}$ 相等时，即为图象横坐标交点，得出x的值，进而得出答案；
③由ax+1- $\text{[math]}$ ＜0，得出ax+1＜ $\text{[math]}$ ，即反比例函数大于一次函数，看在哪些区间反比例函数的图象在上方即可．
点评：本题考查了反比函数综合以及待定系数法的应用，关键要注意根据图象解不等式需从交点看起，图象在上方的对应函数值大．