题目内容
小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________㎝,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?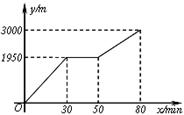
⑴小亮行走的总路程是____________㎝,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?

解:⑴3600,20.
⑵①当 时,设y与x的函数关系式为
时,设y与x的函数关系式为 .
.
根据题意,当 时,
时, ;当
;当 ,
, .
.

所以, 与
与 的函数关系式为
的函数关系式为 .
.
②缆车到山顶的路线长为3600÷2=1800( ),
),
缆车到达终点所需时间为1800÷180=10( ).
).
小颖到达缆车终点时,小亮行走的时间为10+50=60( ).
).
把 代入
代入 ,得y=55×60—800=2500.
,得y=55×60—800=2500.
所以,当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100( ).
).
⑵①当
 时,设y与x的函数关系式为
时,设y与x的函数关系式为 .
.根据题意,当
 时,
时, ;当
;当 ,
, .
.
所以,
 与
与 的函数关系式为
的函数关系式为 .
.②缆车到山顶的路线长为3600÷2=1800(
 ),
),缆车到达终点所需时间为1800÷180=10(
 ).
).小颖到达缆车终点时,小亮行走的时间为10+50=60(
 ).
). 把
 代入
代入 ,得y=55×60—800=2500.
,得y=55×60—800=2500.所以,当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100(
 ).
).(1)纵坐标为小亮行走的路程,其休息的时间为纵坐标不随x的值的增加而增加;
(2)根据当 时函数图象经过的两点的坐标,利用待定系数法求得函数的解析式即可.
时函数图象经过的两点的坐标,利用待定系数法求得函数的解析式即可.
(2)根据当
 时函数图象经过的两点的坐标,利用待定系数法求得函数的解析式即可.
时函数图象经过的两点的坐标,利用待定系数法求得函数的解析式即可.
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 x
x 在函数
在函数 的图象上,且点P在第一象限,点A的坐标为(4,0),设△OPA的面积为S.
的图象上,且点P在第一象限,点A的坐标为(4,0),设△OPA的面积为S. 的解析式表示S,并求出
的解析式表示S,并求出 和
和 .
. 坐标;
坐标; 轴围成的三角形的面积;
轴围成的三角形的面积;
 ,当
,当 ≤x≤1时,y的取值范围为1≤y≤9,则k·b的值为( )
≤x≤1时,y的取值范围为1≤y≤9,则k·b的值为( )
 或21
或21 与x轴、y轴分别交于A、B两点,点C (0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是
与x轴、y轴分别交于A、B两点,点C (0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是  和x>20时y与x的函数表达式;
和x>20时y与x的函数表达式; (元)与从2012年元月份起的月数
(元)与从2012年元月份起的月数 之间的函数关系式以及小亮的存款总数
之间的函数关系式以及小亮的存款总数 (元)与月数
(元)与月数