题目内容
蕲春红人电器行“家电下乡”指定型号的冰箱彩电的进价和售价如下表所示:为满足农民需求,红人电器行决定用不超过85000元采购冰箱和彩电共40台,且冰箱的数量不少于彩电数量的 .
.
| 类别 | 冰箱 | 彩电 |
| 进价(元/台) | 2320 | 1900 |
| 售价(元/台) | 2420 | 1980 |
②哪种进货方案电器行获得的利润最大?(利润=售价-进价)最大利润是多少?
解:①设冰箱采购x台,则彩电采购(40-x)台,根据题意得:
 ,
,
解不等式得:18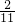 ≤x≤21
≤x≤21 ,
,
∵x为正整数,
∴x=19,20,21,
∴该商场共有3种送货方案,
②设商场获得总利润y元,根据题意得:
y=(2420-2320)x+(1980-1900)(40-x)=20x+3200,
∵20>0,∴y随x的增大而增大,
∴当x=21时,y最大=3620元,
故方案3利润最大,最大利润是3620元.
分析:①利用冰箱总价+彩电总价≤85000;冰箱的数量≥彩电数量的 ;先根据此不等关系求得x的取值范围.
;先根据此不等关系求得x的取值范围.
②总利润为:冰箱总利润+彩电总利润.然后根据自变量的取值选取即可.
点评:此题主要考查了一次函数的应用,解决本题的关键是读懂题意,找到所求量的等量关系,及符合题意的不等关系式.要会利用函数的单调性结合自变量的取值范围求得利润的最大值.
 ,
,解不等式得:18
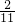 ≤x≤21
≤x≤21 ,
,∵x为正整数,
∴x=19,20,21,
∴该商场共有3种送货方案,
| 冰箱买台 | 彩电买台 | |
| 方案1 | 19 | 21 |
| 方案2 | 20 | 20 |
| 方案3 | 21 | 19 |
y=(2420-2320)x+(1980-1900)(40-x)=20x+3200,
∵20>0,∴y随x的增大而增大,
∴当x=21时,y最大=3620元,
故方案3利润最大,最大利润是3620元.
分析:①利用冰箱总价+彩电总价≤85000;冰箱的数量≥彩电数量的
 ;先根据此不等关系求得x的取值范围.
;先根据此不等关系求得x的取值范围.②总利润为:冰箱总利润+彩电总利润.然后根据自变量的取值选取即可.
点评:此题主要考查了一次函数的应用,解决本题的关键是读懂题意,找到所求量的等量关系,及符合题意的不等关系式.要会利用函数的单调性结合自变量的取值范围求得利润的最大值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目