题目内容
 如图,已知A为DE的中点,设△DBC、△ABC、△EBC的面积分别为S1,S2,S3,则S1、S2、S3之间的关系式是( )
如图,已知A为DE的中点,设△DBC、△ABC、△EBC的面积分别为S1,S2,S3,则S1、S2、S3之间的关系式是( )A、S2=
| ||
B、S2=
| ||
C、S2=
| ||
D、S2=
|
分析:过D,A,E分别作BC得垂线,A为DE的中点,可证AG是四边形DFHE的中位线.分别计算△DBC、△ABC、△EBC的面积可得出三者之间关系.
解答: 解:如图,过D,A,E分别作DF⊥BC,AG⊥CB,EH⊥CB.
解:如图,过D,A,E分别作DF⊥BC,AG⊥CB,EH⊥CB.
则DF∥AG∥EH
∵A为DE的中点
∴AG是四边形DFHE的中位线
∴AG=
(DF+EH).
∵S1=
CB•DF;S2=
CB•AG;S3=
CB•EH;
∴S2=
(S1+S3)
故选C.
 解:如图,过D,A,E分别作DF⊥BC,AG⊥CB,EH⊥CB.
解:如图,过D,A,E分别作DF⊥BC,AG⊥CB,EH⊥CB.则DF∥AG∥EH
∵A为DE的中点
∴AG是四边形DFHE的中位线
∴AG=
| 1 |
| 2 |
∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S2=
| 1 |
| 2 |
故选C.
点评:考查了三角形面积的求法以及梯形中位线的应用.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
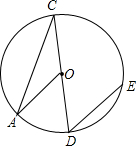 如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )| A、50° | B、40° | C、30° | D、25° |
 19、如图,已知AB为⊙O的直径,DC切⊙O于点C,过D点作 DE⊥AB,垂足为E,DE交AC于点F.求证:△DFC是等腰三角形.
19、如图,已知AB为⊙O的直径,DC切⊙O于点C,过D点作 DE⊥AB,垂足为E,DE交AC于点F.求证:△DFC是等腰三角形. 如图,已知A为DE的中点,设△DBC、△ABC、△EBC的面积分别为S1,S2,S3,则S1、S2、S3之间的关系式是
如图,已知A为DE的中点,设△DBC、△ABC、△EBC的面积分别为S1,S2,S3,则S1、S2、S3之间的关系式是







