题目内容
阅读下列例题:解方程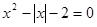
(1)当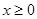 时,原方程化为
时,原方程化为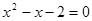 ,解之得
,解之得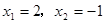 (不符题意,舍去)
(不符题意,舍去)
(2)当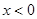 时,原方程化为
时,原方程化为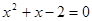 ,解之得
,解之得 (不符题意,舍去)
(不符题意,舍去)
所以原方程的解是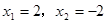
请参照例题解方程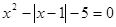 .
.
 ,
,
解析试题分析:先对x的值进行讨论,再去绝对值化简,然后根据一元二次方程的解法解方程即可.
①当 即
即 时,原方程化为
时,原方程化为
解得 ,
, (不符题意,舍去)
(不符题意,舍去)
②当 即
即 时,原方程化为
时,原方程化为
解得 ,
, (不符题意,舍去)
(不符题意,舍去)
所以原方程的解是 ,
, .
.
考点:本题考查了绝对值的性质,解一元二次方程
点评:解答本题的关键是注意当绝对值内的数不小于0时,可直接去掉绝对值,而当绝对值内的数为负数时,去绝对值时,绝对值内的数要变为原来的相反数.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
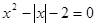
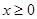 时,原方程化为
时,原方程化为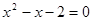 ,解之得
,解之得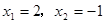 (不符题意,舍去)
(不符题意,舍去)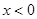 时,原方程化为
时,原方程化为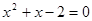 ,解之得
,解之得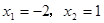 (不符题意,舍去)
(不符题意,舍去)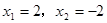
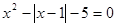 .
.