Question

（本题满分10分）如图，在△ABD和△ACE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．

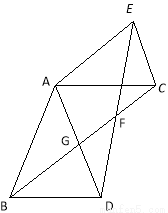
（1）求证：BC=DE；

（2）如果∠ABC=∠CBD ，那么线段FD是线段FG和FB的比例中项吗？为什么？

Answer 1

（1）见解析；（2）是，见解析.

【解析】

试题分析：（1）根据条件证明△BAC≌△DAE即可；（2）根据条件证明△ DFG∽△BFD，利用相似三角形的性质得出比例式，再利用比例的性质得出FD2=FG·FB即可 .

试题解析：（1）证明：

∵∠BAD=∠CAE

∴∠BAC=∠DAE 1分

在△ABC和 △ADE中

∴△BAC≌△DAE 4分

∴BC=DE 5分

（2）、FD是FG和FB的比例中项 6分

理由，由（1）知∠ABC=∠ADE

∵∠ABC =∠CBD

∴∠CBD=∠ADE

又∵∠DFG=∠BFD

∴△ DFG∽△BFD 9分

∴FG:FD=FD:BF

∴FD2=FG·FB 10分

考点：1.全等三角形的判定与性质；2.相似三角形的判定与性质；3. 比例中项.

考点分析： 考点1：图形的相似 形状相同，大小不同的两个图形相似 试题属性

• 题型：
• 难度：
• 考核：
• 年级：