题目内容
(12分)丹东市某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
(1)y=- +24x+3200;
+24x+3200;
(2)应降价200元;
(3)每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
【解析】
试题分析:(1)根据总利润=单件利润×数量列出函数关系式,单件利润=2400-2000-x;数量=8+4× ;(2)根据总利润为4800列出方程进行求解,注意使百姓得到实惠,x要取大的值;(3)根据二次函数的性质求出最大值.
;(2)根据总利润为4800列出方程进行求解,注意使百姓得到实惠,x要取大的值;(3)根据二次函数的性质求出最大值.
试题解析:(1)根据题意,得y=(2400-2000-x)(8+4× ),即y=-
),即y=- +24x+3200
+24x+3200
(2)由题意,得- +24x+3200=4800. 整理,得
+24x+3200=4800. 整理,得 -300x+20000=0
-300x+20000=0
解这个方程,得 =100,
=100, =200. 要使百姓得到实惠,取x=200.
=200. 要使百姓得到实惠,取x=200.
所以,每台冰箱应降价200元.
对于y=- +24x+3200, 当x=-
+24x+3200, 当x=- =150时y最大值
=150时y最大值
 =(2400-200-150)×(8+4×
=(2400-200-150)×(8+4× )=250×20=5000.
)=250×20=5000.
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
考点:一元二次方程与二次函数的应用.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 ,l)关于
,l)关于 轴的对称点为点A1,将OA绕原点O逆时针方向旋转90°到OA2,用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为______.
轴的对称点为点A1,将OA绕原点O逆时针方向旋转90°到OA2,用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为______.


 B.
B. C.
C. D.
D.
 B.6.09×
B.6.09×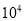 C.609×
C.609×

 = .
= .