Question

【题目】已知点F2 ， P分别为双曲线 的右焦点与右支上的一点，O为坐标原点，若2 |，且 ，则该双曲线的离心率为（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：方法一：设P（x，y），F1（﹣c，0），F2（c，0），
由题意可知：2 = + ，则M为线段PF2的中点，则M（ ， ），
则 =（c，0）， =（ ， ），
则 = ×c= 解得：x=2c，
由丨 丨=丨 丨=c，即 =c，解得：y= c，
则P（2c， c），由双曲线的定义可知：丨PF1丨﹣丨PF2丨=2a，
即 ﹣ =2a，a=（ ﹣1）c，
由双曲线的离心率e= = ，
∴该双曲线的离心率 ，
故选D．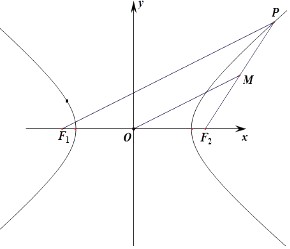
方法二：由题意可知：2 = + ，则M为线段PF2的中点，
则OM为△F2F1P的中位线，
=﹣ =﹣丨 丨丨 丨cos∠OF2M= ，
由丨 丨=丨 丨=c，则cos∠OF2M=﹣ ，
由正弦定理可知：丨OM丨2=丨 丨2+丨 丨2﹣2丨 丨丨 丨cos∠OF2M=3c2 ，
则丨OM丨= c，则丨PF1丨=2 ，丨PF2丨=丨MF2丨=2c，
由双曲线的定义丨PF1丨﹣丨PF2丨=2a，a=（ ﹣1）c，
由双曲线的离心率e= = ，
∴该双曲线的离心率 ，
故选D．
方法一：由题意可知：则M为线段PF2的中点，则M（ ， ），根据向量数量积的坐标运算，即可求得x=2c，利用两点之间的距离公式，即可求得y= c，利用双曲线的定义，即可求得a=（ ﹣1）c，利用双曲线的离心率公式即可求得该双曲线的离心率．
方法二：由题意可知：2 = + ，则M为线段PF2的中点，根据向量的数量积，求得cos∠OF2M，利用余弦定理即可求得丨OM丨，根据三角形的中位线定理及双曲线的定义丨PF1丨﹣丨PF2丨=2a，a=（ ﹣1）c，即可求得双曲线的离心率．