题目内容
18. 如图,AB是⊙O的直径,CB是⊙O的切线,D是⊙O上一点,CD的延长线与BA的延长线交于点E,且CD=CB,证明:CD是⊙O的切线.
如图,AB是⊙O的直径,CB是⊙O的切线,D是⊙O上一点,CD的延长线与BA的延长线交于点E,且CD=CB,证明:CD是⊙O的切线.
分析 连接OD,根据SSS证△ODC≌△OBC,推出∠ODC=∠OBC=90°,根据切线的判定定理推出即可.
解答 证明:连接OD,
在△ODC和△OBC中
$\left\{\begin{array}{l}{CD=CB}\\{OC=OC}\\{OD=OB}\end{array}\right.$,
∴△ODC≌△OBC,
∴∠ODC=∠OBC=90°
∴CD是⊙O的切线.
点评 本题考查了切线的判定,全等三角形的性质和判定,连接圆心O和点D,求出∠ODC=90°是解决问题的关键.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
10.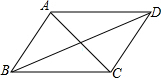 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )| A. | 当AB=AD时,它是菱形 | B. | 当AC=BD时,它是矩形 | ||
| C. | 当AC⊥BD时,它是菱形 | D. | 当∠ABC=90°时,它是正方形 |
7.函数y=4x的图象不经过的点的坐标是( )
| A. | (0,0) | B. | (1,4) | C. | (1,-4) | D. | (-1,-4) |
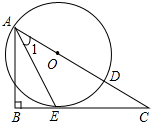 如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.
如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.