题目内容
 古希腊的毕达哥拉斯学派把1,3,6,10,…称为三角形数;把1,4,9,16,…称为数正方形数.“三角形数”和“正方形数”之间存在如下图所示的关系:
古希腊的毕达哥拉斯学派把1,3,6,10,…称为三角形数;把1,4,9,16,…称为数正方形数.“三角形数”和“正方形数”之间存在如下图所示的关系:
即两个相邻的“三角形数”的和为一个“正方形数”,则下列等式符合以上规律的是
- A.6+15=21
- B.36+45=81
- C.9+16=25
- D.30+34=64
B
分析:符合条件的两个三角形数要满足二个条件:两个三角形数之和等于正方形数,两个三角形数之差等于正方形数的平方根.
解答:A、6+15=21,15-6=9≠ ,所以A是错误的;
,所以A是错误的;
B、36+45=81,45-36=9=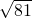 ,所以B是正确的;
,所以B是正确的;
C、9+16=25,16-9=7≠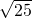 ,所以C是错误的;
,所以C是错误的;
D、30+34=64,34-30=4≠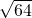 ,所以D是错误的.
,所以D是错误的.
故选B.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
分析:符合条件的两个三角形数要满足二个条件:两个三角形数之和等于正方形数,两个三角形数之差等于正方形数的平方根.
解答:A、6+15=21,15-6=9≠
 ,所以A是错误的;
,所以A是错误的;B、36+45=81,45-36=9=
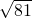 ,所以B是正确的;
,所以B是正确的;C、9+16=25,16-9=7≠
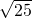 ,所以C是错误的;
,所以C是错误的;D、30+34=64,34-30=4≠
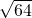 ,所以D是错误的.
,所以D是错误的.故选B.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目