题目内容
已知二次函数 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
(1)求这个二次函数的解析式;
(2)点C是抛物线与 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
(3)在(2)的情况下,求四边形ACQD的面积.
(1)∵二次函数的图像与x轴有两个交点,
∴
∴ .
.
∵m为不小于0的整数,∴m取0、1.
当m=1时, ,图像与x轴的两个交点在原点的同侧,不合题意,舍去;
,图像与x轴的两个交点在原点的同侧,不合题意,舍去;
当m=0时, ,符合题意.
,符合题意.
∴二次函数的解析式为:
(2)∵AC=AD,∴∠ADC=∠ACD
∵CD垂直平分PQ,∴DP=DQ,∴∠ADC=∠CDQ.
∴∠ACD=∠CDQ,∴DQ∥AC
∴△BDQ∽△BAC,∴
∵AC= ,BD=
,BD= ,AB=4.
,AB=4.
∴DQ= ,
,
∴PD= . ∴AP=AD-PD=
. ∴AP=AD-PD= ,
,
∴t=
(3)∵△BDQ∽△BAC
∴
易求 ,∴
,∴
∴ .
.
【解析】(1)根据二次函数的图象与x轴有两个交点,得到△>0,求出m的取值范围,结合m为不小于0的整数,
求出m的整数解;再将整数解代入二次函数解析式,找到符合题意的二次函数;
(2)根据题意画出图象,证出DQ∥AC,从而得到△BDQ∽△BAC,然后利用相似三角形的性质求出t的值;
(3)由于△BDQ∽△BAC,求出 ,利用相似三角形的面积比等于相似比的平方,求出
,利用相似三角形的面积比等于相似比的平方,求出 ,二者相减,即可得到
,二者相减,即可得到

 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值; 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边. 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;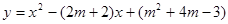 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边. 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值; 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边. 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;