题目内容
7．在Rt△ABC中，∠C=90°，若AC=2BC，则cosA的值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |
分析 根据勾股定理，可得AB与BC的关系，根据余弦函数的定义，可得答案．
解答 解：由勾股定理，得
AB=$\sqrt{5}$BC．
由余弦函数的定义，得
cosA=$\frac{AC}{AB}$=$\frac{2BC}{\sqrt{5}BC}$=$\frac{2\sqrt{5}}{5}$，
故选：D．
点评 本题考查了锐角三角函数的定义，先利用勾股定理得出BA与BC的关系，再利用余弦函数的定义．
练习册系列答案
相关题目
如图所示，A、B两地位于某高速铁路沿线（直线）的两侧．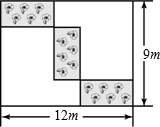
在长为12m，宽为9m的长方形空地上，沿平行于长方形各边的方向分别割出三个大小完全一样的小长方形花圃，其示意图如图所示，求其中一个小长方形花圃的长和宽．
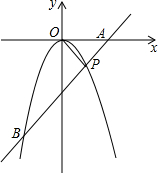如图，抛物线y=ax2（a≠0）与直线AB交于点P（4，-4），连接OP，则OP=AP，求二次函数的解析式及抛物线与直线AB另一个交点B的坐标．
19．下列各数中无理数是（ ）
| A． | $\frac{7}{11}$ | B． | -1 | C． | 0 | D． | $\frac{π}{3}$ |
16．某种生物细胞的直径是0.000000012cm，用科学记数法表示这个数，正确的是（ ）
| A． | 12×10-7cm | B． | 1.2×10-7cm | C． | 12×10-8cm | D． | 1.2×10-8cm |
17．因式分解x3-4x的结果是（ ）
| A． | x（x2-4） | B． | x（x-4）2 | C． | x（x-2）（x+2） | D． | x（x-2）2 |