题目内容
17．
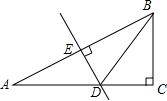如图所示，在Rt△ABC中，∠C=90°，AB的垂直平分线交AC于D，交AB于E，若∠A=28°，求∠ABD和∠CBD的度数．
分析 根据线段垂直平分线性质得出AD=BD，推出∠ABD=∠A=28°，根据三角形外角性质求出∠CDB，根据三角形内角和定理求出即可．
解答 解：∵AB的垂直平分线交AC于D，交AB于E，∠A=28°，
∴AD=BD，
∴∠ABD=∠A=28°，
∴∠CDB=∠A+∠ABD=28°+28°=56°，
∵∠C=90°，
∴∠CBD=90°-∠CDB=90°-56°=34°．
点评 本题考查了线段垂直平分线性质，等腰三角形的性质，三角形外角性质，三角形的内角和定理的应用，能灵活运用定理进行推理和计算是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
相关题目
如图，在一块长AB=a cm，宽BC=b cm的长方形草地上，有三条宽都是2m的小路，则这块草地的绿地面积为（a-4）（b-2）cm2．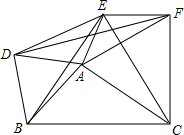
如图，以△ABC的三边为边在BC的同一侧分别作三个等边三角形，即△ABD、△BCE、△ACF，且∠BAC≠60°．
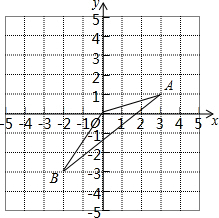如图，已知A（3，1），B（-2，-3）．
如图，在平面直角坐标系中，已知点A（-3，4），B（-1，-2），O为原点，求△AOB的面积．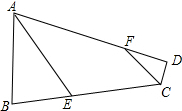
如图，在四边形ABCD中，AE，CF分别是∠BAD，∠BCD的平分线，分别交BC，AD于点E，F．
6．下列正多边形中，外角和等于内角和的是（ ）
| A． | 正三角形 | B． | 正四边形 | C． | 正六边形 | D． | 正八边形 |