题目内容
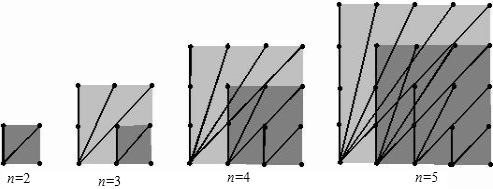
探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:

当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,![]() ,2,
,2,![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5。
五种,比n=2时增加了3种,即S=2+3=5。
(1) 观察图形,填写下表:
| 钉子数(n×n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
(2) 写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式。
解:(1)4,2+3+4+5(或14)
(2)(i)n×n的钉子板比(n-1)×(n-1)的钉子板中不同长度的线段种数增加了n种;
(ii)分别用a,b表示n×n与(n-1)×(n-1)的钉子板中不同长度的线段种数,
则a=b+n。
(3)S=2+3+4+…+n

练习册系列答案
相关题目
探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,
,2,
,2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式.
当n=2时,钉子板上所连不同线段的长度值只有1与
| 2 |
当n=3时,钉子板上所连不同线段的长度值只有1,
| 2 |
| 5 |
| 2 |
(1)观察图形,填写下表:
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式.

| 钉子数(n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。
 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2; ,2
,2
 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,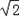 ,2,
,2, ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
