Question

【题目】已知△ABC中，∠BAC＝90°，AB＝AC．

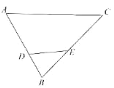
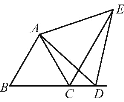
（1）如图，D为AC上任一点，连接BD，过A点作BD的垂线交过C点与AB平行的直线CE于点E．求证：BD＝AE．

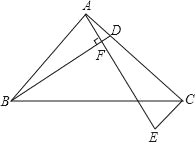
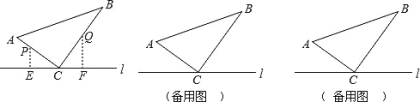
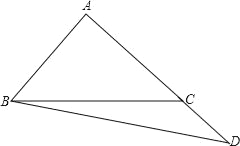
（2）若点D在AC的延长线上，如图，其他条件同（1），请画出此时的图形，并猜想BD与AE是否仍然相等？说明你的理由．

Answer 1

【答案】证明：（1）∵AB∥CE，

∴∠BAF=∠AEC，∠BAC+∠ACE=180°，

∵∠BAC=90°，

∴∠ACE=90°，

∵AF⊥BD，

∴∠ABD+∠BAF=90°，∠EAC+∠BAF=90°，

∴∠ABD=∠CAE

在△ABD和△CAE中，

AB="AC" ∠BAC=∠ACE ∠AEC=∠ABD ∴△ABD≌△CAE（AAS）

∴BD=AE．

（2）BD与AE仍然相等，

证明：过点C作AB∥CE，过点A作AE⊥BD于点F，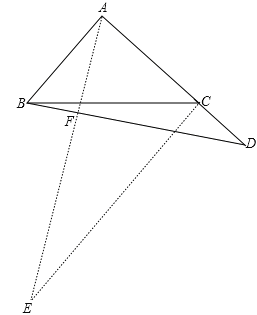

∵AB∥CE，

∴∠BAF=∠AEC，∠BAC+∠ACE=180°，

∵∠BAC=90°，

∴∠ACE=90°，

，∵AF⊥BD，

∴∠ABD+∠BAF=90°，∠EAC+∠BAF=90°，

∴∠ABD=∠CAE

在△ABD和△CAE中，

AB="AC" ∠BAC=∠ACE ∠AEC=∠ABD

∴△ABD≌△CAE（AAS）

∴BD=AE．

【解析】

（1）先证∠ABD=∠CAE，再证△ABD≌△CAE即可得出答案．

（2）根据题意画出图形，然后可根据△ABD≌△ACE得出结论