题目内容
 6、将正整数从1开始依次按如图所示的规律排成一个数阵,其中,2在第1个拐角处,3在第2个拐角处,5在第3个拐角处,7在第4个拐角处,….那么,在第2007个拐角处的数是
6、将正整数从1开始依次按如图所示的规律排成一个数阵,其中,2在第1个拐角处,3在第2个拐角处,5在第3个拐角处,7在第4个拐角处,….那么,在第2007个拐角处的数是1008017
.分析:依次得到每个拐弯处的数与第n个拐弯的关系,得到相应规律,代入计算即可.
解答:解:第1个拐弯:1+1=2
第2个拐弯:1+1+1=3
第3个拐弯:1+1+1+2=5
第4个拐弯:1+1+1+2+2=1+(1+2)×2=7
第5个拐弯:1+1+1+2+2+3=1+(1+2)×2+3=10
第6个拐弯:1+1+1+2+2+3+3=1+(1+2+3)×2=13
第7个拐弯:1+1+1+2+2+3+3+4=1+(1+2+3)×2+4=17
…
∵2007=2×1 003+1,
∴A(2007)=1+(1+2+3+…+1003)×2+1004
=1008017
故答案为1008017.
第2个拐弯:1+1+1=3
第3个拐弯:1+1+1+2=5
第4个拐弯:1+1+1+2+2=1+(1+2)×2=7
第5个拐弯:1+1+1+2+2+3=1+(1+2)×2+3=10
第6个拐弯:1+1+1+2+2+3+3=1+(1+2+3)×2=13
第7个拐弯:1+1+1+2+2+3+3+4=1+(1+2+3)×2+4=17
…
∵2007=2×1 003+1,
∴A(2007)=1+(1+2+3+…+1003)×2+1004
=1008017
故答案为1008017.
点评:考查数字的变化规律;得到第n个拐弯处=1+[1+2+3…+(n-1)÷2]+(n+1)÷2的规律是解决本题的关键.

练习册系列答案
相关题目
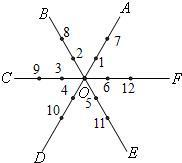 16、如图,平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为
16、如图,平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为
 将正整数从1开始依次按如图所示的规律排成一个数阵,其中,2在第1个拐角处,3在第2个拐角处,5在第3个拐角处,7在第4个拐角处,….那么,在第2007个拐角处的数是________.
将正整数从1开始依次按如图所示的规律排成一个数阵,其中,2在第1个拐角处,3在第2个拐角处,5在第3个拐角处,7在第4个拐角处,….那么,在第2007个拐角处的数是________.