题目内容
16.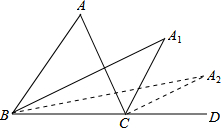 如图,△A1BC一个内角的平分线和一个外角的平分线相交得到点A2,△A2BC的内外角平分线相交,得到点A3,…,用∠A表示∠A2015.
如图,△A1BC一个内角的平分线和一个外角的平分线相交得到点A2,△A2BC的内外角平分线相交,得到点A3,…,用∠A表示∠A2015.
分析 由三角形的外角性质知:∠A=∠ACD-∠ABC,而∠A1=$\frac{1}{2}$(∠ACD-∠ABC),即∠A1=$\frac{1}{2}$∠A,同理可得,∠A2=$\frac{1}{2}$∠A1,依此类推即可.
解答 解:△ABC中,∵∠A=∠ACD-∠ABC,A1是∠ABC角平分与∠ACD的平分线的交点,
∴∠A1=∠A1CD-∠A1BC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A;
同理可得,∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,
∠A3=$\frac{1}{2}$∠A2=$\frac{1}{{2}^{3}}$∠A,
…
依此类推,∠An=$\frac{1}{{2}^{n}}$∠A.
则∠A2015=$\frac{1}{{2}^{2015}}$∠A.
点评 本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和是180°和三角形的一个外角等于与它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
6.若(b-1)2+a2=0,则下列方程中是关于x的一元二次方程的是( )
| A. | ax2+5x-b=0 | B. | (b2-1)x2+(a+3)x-5=0 | C. | (a-1)x2+(b-1)x-7=0 | D. | (b-1)x2+ax-1=0 |
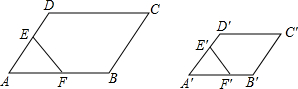 如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.
如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′. 已知a,b在数轴上的位置如图所示.
已知a,b在数轴上的位置如图所示.