题目内容
1. 甲、乙两人相约从A地到B地,甲骑自行车先行,乙开汽车,两人均在同一路线上匀速行驶,乙到B地后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为$\frac{5}{8}$小时.
甲、乙两人相约从A地到B地,甲骑自行车先行,乙开汽车,两人均在同一路线上匀速行驶,乙到B地后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为$\frac{5}{8}$小时.
分析 根据速度=路程÷时间,可求甲骑自行车的速度为20÷1=20千米/小时,根据速度差=路程差÷追击时间可求乙开汽车的速度,再根据追击时间=路程差÷速度差可求乙追上甲后到达B地的时间,再把两个时间相加即可求解.
解答 解:20÷1=20(千米/小时),
20÷($\frac{5}{4}$-1)+20
=20÷$\frac{1}{4}$+20
=80+20
=100(千米/小时),
30÷(100-20)+($\frac{5}{4}$-1)
=30÷80+$\frac{1}{4}$
=$\frac{3}{8}$+$\frac{1}{4}$
=$\frac{5}{8}$(小时).
答:乙从A地到B地所用的时间为$\frac{5}{8}$小时.
故答案为:$\frac{5}{8}$.
点评 本题考查了一次函数的应用,解决本题的关键是根据图象获取相关信息,利用追击问题的关系式得到乙开汽车的速度.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.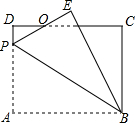 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )| A. | 4.8 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 3$\sqrt{3}$ |
13.由$\frac{4y-3x}{2}=1$,可以得到用y表示x的式子( )
| A. | y=$\frac{3x-2}{4}$ | B. | 3x=4y-2 | C. | x=$\frac{4y-2}{3}$ | D. | x=$\frac{2-4y}{3}$ |
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.