Question

【题目】如图，直线∥ ，⊙O与和分别相切于点A和点B．点M和点N分别是和上的动点，MN沿和平移．⊙O的半径为1，∠1＝60°．下列结论错误的是（　　）

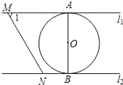
A. B. l1和l2的距离为2

C. 若∠MON＝90°，则MN与⊙O相切 D. 若MN与⊙O相切，则

Answer 1

【答案】D

【解析】

首先过点N作NC⊥AM于点C，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B，⊙O的半径为1，易求得MN= = ，l1和l2的距离为2；
若∠MON=90°，连接NO并延长交MA于点C，易证得CO=NO，继而可得即O到MN的距离等于半径，可证得MN与⊙O相切；
由题意可求得若MN与⊙O相切，则AM=或．

解：如图1，过点N作NC⊥AM于点C，

∵直线l1∥l2，⊙O与l1和l2分别相切于点A和点B，⊙O的半径为1，

∴CN＝AB＝2，

∵∠1＝60°，

∴MN＝ =，

故A与B正确；

如图3，

若∠MON＝90°，连接NO并延长交MA于点C，则△AOC≌△BON，

故CO＝NO，△MON≌△MOM′，故MN上的高为1，即O到MN的距离等于半径．

故C正确；

如图2，∵MN是切线，⊙O与l1和l2分别相切于点A和点B，

∴∠AMO＝∠1＝30°，

∴AM＝；

∵∠AM′O＝60°，

∴AM′＝，

∴若MN与⊙O相切，则AM＝或；

故D错误．

故选：D．