题目内容
下列命题是真命题的是（ ）
| A、三角形的外角大于任何一个三角形的内角 |
| B、全等三角形的面积相等，周长相等 |
| C、直角三角形只有一条高 |
| D、有两个角和一条边相等的两个三角形全等 |
考点：命题与定理
专题：
分析：利用三角形的外角的性质、全等三角形的性质及三角形全等的判定分别判断后即可确定正确的选项．
解答：解：A、三角形的外角大于任何一个与之不相邻的内角，故选项错误；
B、全等三角形的面积相等，周长相等，故选项正确；
C、直角三角形也有三条高，故选项错误；
D、有两个角和一条边相等的两个三角形全等，故选项错误．
故选B．
B、全等三角形的面积相等，周长相等，故选项正确；
C、直角三角形也有三条高，故选项错误；
D、有两个角和一条边相等的两个三角形全等，故选项错误．
故选B．
点评：本题考查了三角形的外角的性质、全等三角形的性质及三角形全等的判定，难度不大，都是些基础定义及定理．
练习册系列答案
应用题作业本系列答案
相关题目
三角形的两条边长为3cm和6cm，下列长度中，可能是这个三角形第三条边的是（ ）
| A、3cm | B、5cm |
| C、9cm | D、12cm |
如果a-5b=-3，那么代数式5-a+5b的值是（ ）
| A、0 | B、2 | C、5 | D、8 |
14：00时，时针和分针所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
若a、b互为相反数，则关于x的方程ax+b=0（a≠0）的解是（ ）
| A、x=1 | B、x=-1 |
| C、x=1或x=-1 | D、不能确定 |
同一平面内，有三条不同的直线，如果它们两两相交，则交点的个数只能是（ ）
| A、1个 | B、2个 |
| C、3个 | D、1或3个 |
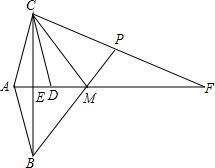已知：如图，三角形ABM与三角形ACM关于直线AF成轴对称，三角形ABE与三角形DCE关于点E成中心对称，点E、D、M都在线段AF上，BM的延长线交CF于点P．