题目内容
如图3312，已知一次函数y1＝kx＋b与反比例函数y2＝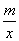
的图象交于A(2,4)，B(－4，n)两点．
(1)分别求出y1和y2的解析式；
(2)写出当y1＝y2时，x的值；
(3)写出当y1＞y2时，x的取值范围．
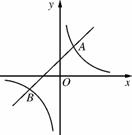
图3312
解：(1)将A(2,4)代入反比例解析式，得m＝8，
∴反比例函数解析式为y2＝
.
将B(－4，n)代入反比例解析式，得n＝－2，
即B(－4，－2)，
将点A与点B坐标代入一次函数解析式，得
解得
则一次函数解析式为y1＝x＋2.
(2)联立两函数解析式，得
解得
或
则当y1＝y2时，x的值为2或－4.
(3)利用图象，得当y1＞y2时，x的取值范围为－4＜x＜0或x＞2.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
，b＝|－2|，c＝
，求代数式a2＋b－4c的值．
，下列说法正确的是( )
的图象关于y轴成轴对称，则该函数的解析式为__________．
＝________；
＝________.