题目内容
 如图,点A、C、E在反比例函数
如图,点A、C、E在反比例函数 的图象上,AB⊥x轴于点B,CD⊥x轴于点D,EF⊥x轴于点F,△AOB,△COD,△EOF的面积分别为S1,S2,S3,则
的图象上,AB⊥x轴于点B,CD⊥x轴于点D,EF⊥x轴于点F,△AOB,△COD,△EOF的面积分别为S1,S2,S3,则
- A.S1>S2>S3
- B.S1<S2<S3
- C.S3>S1>S2
- D.S1=S2=S3
D
分析:根据图形、三角形的面积公式(反比例函数系数k的几何意义)易得,△AOB,△COD,△EOF的面积相等,可得S1,S2,S3的大小关系.
解答:设点A的坐标为(xA,yA),点B的坐标为(xB,yB),点C的坐标为(xC,yC),
∵A、B在反比例函数y= 上,
上,
∴xAyA=6,xByB=6,xCyC=6,
∴S△AOB= xAyA=3;S△ODC=
xAyA=3;S△ODC= xByB=3,S△OEF=
xByB=3,S△OEF= xCyC=3,
xCyC=3,
∴S△AOB=S△ODC=S△OEF,
∴S1=S2=S3.
故选:D.
点评:本题考查了反比例函数系数k的几何意义.解答本题时采用了“数形结合”的数学思想.
分析:根据图形、三角形的面积公式(反比例函数系数k的几何意义)易得,△AOB,△COD,△EOF的面积相等,可得S1,S2,S3的大小关系.
解答:设点A的坐标为(xA,yA),点B的坐标为(xB,yB),点C的坐标为(xC,yC),
∵A、B在反比例函数y=
 上,
上,∴xAyA=6,xByB=6,xCyC=6,
∴S△AOB=
 xAyA=3;S△ODC=
xAyA=3;S△ODC= xByB=3,S△OEF=
xByB=3,S△OEF= xCyC=3,
xCyC=3,∴S△AOB=S△ODC=S△OEF,
∴S1=S2=S3.
故选:D.
点评:本题考查了反比例函数系数k的几何意义.解答本题时采用了“数形结合”的数学思想.

练习册系列答案
相关题目
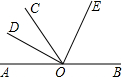 如图,点A,O,B在同一直线上,射线OD平分∠AOC,射线OE平分∠BOC.
如图,点A,O,B在同一直线上,射线OD平分∠AOC,射线OE平分∠BOC. 如图,点A、B、C在⊙O上,AO∥BC,∠OBC=40°,则∠ACB的度数是
如图,点A、B、C在⊙O上,AO∥BC,∠OBC=40°,则∠ACB的度数是 (2012•北京)已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.
(2012•北京)已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD. (2012•鞍山)如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
(2012•鞍山)如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP. (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y=