Question

如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；
（2）五边形ACBB′C′的周长为______；
（3）四边形ACBB′的面积为______；
（4）在直线l上找一点P，使PB+PC的长最短，则这个最短长度为______．

Answer 1

解：（1）如图：△AB′C′即为所求；

（2）∵AC′=AC==2，BC=BC′==，BB′=2，
∴五边形ACBB′C′的周长为：2×2+2×+2=4+2+2；
故答案为：4+2+2；

（3）如图，S_△ABC=S_梯形AEFB-S_△AEC-S_△BCF=×（1+2）×4-×2×2-×2×1=3，S_△ABB′=×2×4=4，
∴S_{四边形ACBB′}=S_△ABC+S_△ABB′=3+4=7．
故答案为：7；

（4）如图，点B′是点B关于l的对称点，连接B′C，交l于点P，
此时PB+PC的长最短，
∴PB=PB′，
∴PB+PC=PB′+PC=B′C==．
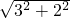故答案为：．
分析：（1）根据轴对称的性质，可作出△ABC关于直线l成轴对称的△AB′C′；
（2）由勾股定理即可求得AC与BC的长，由对称性，可求得其它边长，继而求得答案；
（3）由S_△ABC=S_梯形AEFB-S_△AEC-S_△BCF，可求得△ABC的面积，易求得△ABB′的面积，继而求得答案；
（4）由点B′是点B关于l的对称点，连接B′C，交l于点P，然后由B′C的长即可．
点评：此题考查了轴对称变换、三角形的面积以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．