题目内容
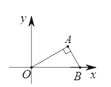
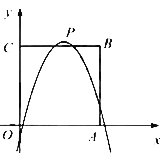
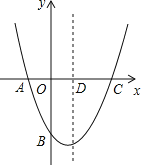
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx-![]() 的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)M(s,t)为抛物线对称轴上的一个动点,
①若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,直接写出点M的坐标;
②连接MA、MB,若∠AMB不小于60°,求t的取值范围.
【答案】(1)y=![]() x2-
x2-![]() x-
x-![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() )(2)①(
)(2)①(![]() ,
,![]() ),(
),(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() )②
)②![]() ≤t≤
≤t≤![]()
【解析】
(1)根据二次函数y=ax2+bx-![]() 的图象经过点A(-1,0)、C(2,0),可以求得该函数的解析式,然后将函数解析式化为顶点式,即可得到该函数的顶点坐标;
的图象经过点A(-1,0)、C(2,0),可以求得该函数的解析式,然后将函数解析式化为顶点式,即可得到该函数的顶点坐标;
(2)①根据题意,画出相应的图形,然后利用分类讨论的方法即可求得点M的坐标;
②根据题意,构造一个圆,然后根据圆周角与圆心角的关系和∠AMB不小于60°,即可求得t的取值范围.
(1)∵二次函数y=ax2+bx-![]() 的图象经过点A(-1,0)、C(2,0),
的图象经过点A(-1,0)、C(2,0),
∴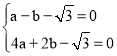 ,得
,得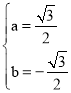 ,
,
∴y=![]() x2-
x2-![]() x-
x-![]() =
=![]() ,
,
∴二次函数的表达式是y=![]() x2-
x2-![]() x-
x-![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() );
);
(2)①点M的坐标为(![]() ,
,![]() ),(
),(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() )
)
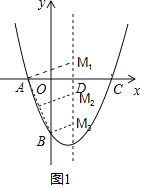
理由:当AM1⊥AB时,如右图1所示,
∵点A(-1,0),点B(0,-![]() ),
),
∴OA=1,OB=![]() ,
,
∴tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=60°,
∴∠OAM1=30°,
∴tan∠OAM1=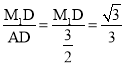 ,
,
解得,DM1=![]() ,
,
∴M1的坐标为(![]() ,
,![]() );
);
当BM3⊥AB时,
同理可得,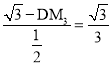 ,解得,DM3=
,解得,DM3=![]() ,
,
∴M3的坐标为(![]() ,-
,-![]() );
);
当点M2到线段AB的中点的距离等于线段AB的一半时,
∵点A(-1,0),点B(0,-![]() ),
),
∴线段AB中点的坐标为(-![]() ),线段AB的长度是2,
),线段AB的长度是2,
设点M2的坐标为(![]() ,m),
,m),
则![]() =1,解得,m=
=1,解得,m=![]() ,
,
即点M2的坐标为(![]() ,-
,-![]() );
);
由上可得,点M的坐标为(![]() ,
,![]() ),(
),(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() );
);
②如图2所示,作AB的垂直平分线,于y轴交于点F,

由题意知,AB=2,∠BAF=∠ABO=30°,∠AFB=120°,
∴以F为圆心,AF长为半径作圆交对称轴于点M和M′点,
则∠AMB=∠AM′B=![]() ∠AFB=60°,
∠AFB=60°,
∵∠BAF=∠ABO=30°,OA=1,
∴∠FAO=30°,AF=![]() =FM=FM′,OF=
=FM=FM′,OF=![]() ,
,
过点F作FG⊥MM′于点G,
∵FG=![]() ,
,
∴MG=M′G=![]() ,
,
又∵G(![]() ,-
,-![]() ),
),
∴M(![]() ,
,![]() ),M′(
),M′(![]() ,
,![]() ),
),
∴![]() ≤t≤
≤t≤![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案