题目内容
 已知等边△ABC的周长为6厘米,求它的面积.
已知等边△ABC的周长为6厘米,求它的面积.分析:先根据等边△ABC的周长为6厘米求出BC的长,再过点A作AD⊥BC,求出AD的长,利用三角形的面积公式求解即可.
解答: 解:∵等边△ABC的周长为6厘米,
解:∵等边△ABC的周长为6厘米,
∴AB=BC=
=2cm,
过点A作AD⊥BC于点D,则AD=AB•sin60°=2×
=
,
∴S△ABC=
BC•AD=
×2×
=
(平方厘米).
答:它的面积是
平方厘米.
 解:∵等边△ABC的周长为6厘米,
解:∵等边△ABC的周长为6厘米,∴AB=BC=
| 6 |
| 3 |
过点A作AD⊥BC于点D,则AD=AB•sin60°=2×
| ||
| 2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
答:它的面积是
| 3 |
点评:本题考查的是等边三角形的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
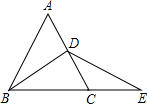 如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是( )
如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是( )A、5+2
| ||
B、5+
| ||
C、3+2
| ||
D、3+
|







 B.
B. C.
C. D.
D.