Question

如图，Rt△ABC中，∠ACB=90°，CA=3cm，CB=4cm，设点P、Q为AB、CB上动点，它们分别从A、C同时出发向B点匀速移动，移动速度为1cm/秒，设P、Q移动时间为t秒（0≤t≤4）．
①当∠CPQ=90°时，求t的值．
②是否存在t，使△CPQ成为正三角形？若存在，求出t的值；若不存在，能否改变Q的运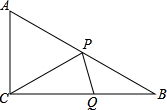动速度（P的速度不变），使△CPQ成为正三角形？如何改变？并求出相应的t值．

Answer 1

解：①过P作MP⊥AC与M，作PN⊥CB于N，如图，AP=CQ=t，
∵∠ACB=90°，CA=3cm，CB=4cm，
∴AB=5cm，PM∥BC，
∴△APM∽△ACB，
∴MP：BC=AM：AC=AP：AB，
∴MP=t，AM=t，
∴CM=3-t，
在Rt△PCM中，PC²=PM²+MC²=（t）²+（3-t）²=t²-t+9，
又CN=PM=t，
∵∠CPQ=90°，
∴Rt△CPN∽Rt△CQP，
∴CP：CQ=CN：CP，即CP²=CN•CQ，
∴t²-t+9=（t）•t，整理得：t²-18t+45=0，
∴t₁=3（t₂=15舍去），
∴当∠CPQ=90°时，t的值为3；

②ⅰ）假设存在t使△PCQ为正三角形．
∴PN平分CQ，即CN=CQ=t，
∵CN=MP，
∴t=t
∴t=0，
∴△PCQ不存在，
即△CPQ不可能为正三角形；
ⅱ）设Q的速度为x，则CQ=xt，
若△CPQ为正三角形，CN=CQ=xt，
而CN=PM，即xt=t，
∴x=，
∴CQ=t，
∵PN=CQ，PN=CM，
∴3-t=•t，
∴t=．
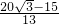∴不存在t，使△CPQ成为正三角形，
当Q的运动速度为cm/秒（P的速度不变），使△CPQ成为正三角形，相应的t值为．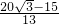
分析：①过P作MP⊥AC与M，作PN⊥CB于N，易得AB=5cm，PM∥BC，利用△APM∽△ACB的相似比可表示出MP=t，AM=t，则CM=3-t，在Rt△PCM中利用勾股定理得到PC²=PM²+MC²=（t）²+（3-t）²=t²-t+9；又Rt△CPN∽Rt△CQP，得到CP²=CN•CQ=t•t，由此可得到关于t的一元二次方程，解方程即可得到t的值；
②假设存在t使△PCQ为正三角形，CN=CQ=t，而CN=MP，得到t=t，解得t=0不合题意；设Q的速度为x，则CQ=xt，若△CPQ为正三角形，CN=CQ=xt，而CN=MP=t，可得到x=，然后根据等边三角形的高为边长的倍得到3-t=•t，解方程求得满足条件的t的值．
点评：本题考查了三角形相似的判定与性质：有两组角对应相等的两个三角形相似；相似三角形对应边的比相等．也考查了等边三角形的性质以及勾股定理．