题目内容
 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠BCD=45°,点E在BC上,且∠AEB=60°.若AB=2
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠BCD=45°,点E在BC上,且∠AEB=60°.若AB=2| 3 |
考点:梯形,勾股定理
专题:计算题
分析:过点D作DF⊥BC,根据∠BCD=45°,得DF=CF,再由AB=2
,可得DF=CF=2
,由勾股定理得CD的长,因为AD=1,所以BC=2
+1,根据∠AEB=60°,可得BE,进而得出CE的长.
| 3 |
| 3 |
| 3 |
解答: 解:过点D作DF⊥BC,
解:过点D作DF⊥BC,
∵AD∥BC,∠ABC=90°,
∴四边形ABFD为矩形,
∵∠BCD=45°,
∴DF=CF,
∵AB=2
,
∴DF=CF=2
,
∴由勾股定理得CD=2
;
∵AD=1,
∴BF=1,
∴BC=2
+1,
∵∠AEB=60°,
∴tan60°=
,
∴
=
,
∴BE=2,
∴CE=BC-BE=2
+1-2=2
-1.
 解:过点D作DF⊥BC,
解:过点D作DF⊥BC,∵AD∥BC,∠ABC=90°,
∴四边形ABFD为矩形,
∵∠BCD=45°,
∴DF=CF,
∵AB=2
| 3 |
∴DF=CF=2
| 3 |
∴由勾股定理得CD=2
| 6 |
∵AD=1,
∴BF=1,
∴BC=2
| 3 |
∵∠AEB=60°,
∴tan60°=
| AB |
| BE |
∴
2
| ||
| BE |
| 3 |
∴BE=2,
∴CE=BC-BE=2
| 3 |
| 3 |
点评:本题考查了梯形的计算以及勾股定理,是基础知识要熟练掌握.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 如图,在△ABC中,BD⊥AC,AB=6,AC=5
如图,在△ABC中,BD⊥AC,AB=6,AC=5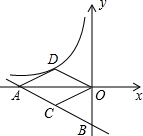 如图,一次函数y=-
如图,一次函数y=-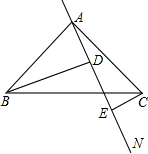 如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.
如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由. 如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是
如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是