题目内容
矩形ABCD对角线AC、BD相交于O,AE平分∠BAD交矩形一边于E,若∠CAE=15°,则∠BOC= .
【答案】分析:根据∠CAE=15°和AE平分∠BAD,即可求得∠BAO=60°,再根据OA=OB即可判定△ABO为等边三角形,即可求∠AOB,进而求出∠BOC的度数.
解答:解:∵∠CAE=15°和AE平分∠BAD,
∴∠BAO=45°+15°=60°,
又∵AO=BO,
∴△ABO为等边三角形,
∴∠AOB=60°,
∴∠BOC=180°-60°=120°.
故答案为:120°.
点评:本题考查了矩形对角线相等且互相平分的性质,考查了等边三角形的判定和等边三角形各内角为60°的性质,本题中求证△ABO为等边三角形是解题的关键.
解答:解:∵∠CAE=15°和AE平分∠BAD,
∴∠BAO=45°+15°=60°,
又∵AO=BO,
∴△ABO为等边三角形,
∴∠AOB=60°,
∴∠BOC=180°-60°=120°.
故答案为:120°.
点评:本题考查了矩形对角线相等且互相平分的性质,考查了等边三角形的判定和等边三角形各内角为60°的性质,本题中求证△ABO为等边三角形是解题的关键.

练习册系列答案
相关题目
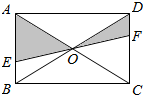 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,E F过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,则S阴影是S矩形ABCD的( )
如图,E F过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,则S阴影是S矩形ABCD的( )A、
| ||
B、
| ||
C、
| ||
D、
|
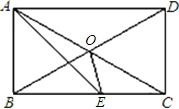 已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=
已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,∠AEO=
 (2012•广州模拟)矩形ABCD对角线AC、BD相交于O,AE平分∠BAD交矩形一边于E,若∠CAE=15°,则∠BOC=
(2012•广州模拟)矩形ABCD对角线AC、BD相交于O,AE平分∠BAD交矩形一边于E,若∠CAE=15°,则∠BOC=